题目内容
【题目】若无穷数列![]() 满足:
满足:![]() 是正实数,当
是正实数,当![]() 时,
时,![]() ,则称
,则称![]() 是“
是“![]() —数列”.
—数列”.
(1)若![]() 是“
是“![]() —数列”且
—数列”且![]() ,写出
,写出![]() 的所有可能值;
的所有可能值;
(2)设![]() 是“
是“![]() —数列”,证明:
—数列”,证明:![]() 是等差数列当且仅当
是等差数列当且仅当![]() 单调递减;
单调递减;![]() 是等比数列当且仅当
是等比数列当且仅当![]() 单调递增;
单调递增;
(3)若![]() 是“
是“![]() —数列”且是周期数列(即存在正整数
—数列”且是周期数列(即存在正整数![]() ,使得对任意正整数
,使得对任意正整数![]() ,都有
,都有![]() ),求集合
),求集合![]() 的元素个数的所有可能值的个数.
的元素个数的所有可能值的个数.
【答案】(1)-2,0,2,8(2)证明见解析(3)当![]() 时,有32种;当
时,有32种;当![]() 时,有31种.
时,有31种.
【解析】
(1)根据“![]() —数列”的定义逐项分析即可.
—数列”的定义逐项分析即可.
(2)分别根据等差等比数列的定义,分别证明对应的必要性和充分性即可.
(3)分别证明![]() 是数列
是数列![]() 中的最大项与当
中的最大项与当![]() 是奇数时,
是奇数时,![]() 是
是![]() 的奇数倍;当
的奇数倍;当![]() 是偶数时,
是偶数时,![]() 是
是![]() 的偶数倍再根据周期的性质证明即可.
的偶数倍再根据周期的性质证明即可.
(1)解:由题,所有可能的情况有![]() ,
,![]() ,
,![]() .
.
故![]() 的所有可能值为 -2,0,2,8.
的所有可能值为 -2,0,2,8.
(2)证明:因为![]() ,所以
,所以![]() 或
或![]() .
.
当![]() 是等差数列时,假设
是等差数列时,假设![]() ,则
,则![]() ,此时,
,此时,![]() ,而
,而![]() ,矛盾!所以
,矛盾!所以![]() .于是公差
.于是公差![]() ,所以
,所以![]() 单调递减.
单调递减.
当![]() 单调递减时,对任意
单调递减时,对任意![]() ,
,![]() ,又
,又![]() ,所以
,所以![]() ,从而
,从而![]() 是等差数列.
是等差数列.
当![]() 是等比数列时,
是等比数列时,![]() ,所以
,所以![]() ,于是公比
,于是公比![]() .又
.又![]() ,所以
,所以![]() 单调递增.
单调递增.
当![]() 单调递增时,对任意
单调递增时,对任意![]() ,
,![]() .又
.又![]() ,所以
,所以![]() ,即
,即![]() .因为
.因为![]() ,所以
,所以![]() 是等比数列.
是等比数列.
(3)解:先证明![]() 是数列
是数列![]() 中的最大项.
中的最大项.
事实上,如果![]() 是第一个大于
是第一个大于![]() 的项的脚标,则由
的项的脚标,则由
![]()
知,![]() 是
是![]() 的倍数.假设
的倍数.假设![]() ,
,![]() ,…,
,…,![]() 都是
都是![]() 的倍数,则由
的倍数,则由
![]()
![]()
知,![]() 也是
也是![]() 的倍数.所以由归纳法知,对任意
的倍数.所以由归纳法知,对任意![]() ,
,![]() 都是
都是![]() 的倍数,但
的倍数,但![]() 不是
不是![]() 的倍数,这与
的倍数,这与![]() 是周期数列矛盾!
是周期数列矛盾!
所以![]() 是数列
是数列![]() 中的最大项,从而当
中的最大项,从而当![]() 时,
时,![]() .
.
再证明当![]() 是奇数时,
是奇数时,![]() 是
是![]() 的奇数倍;当
的奇数倍;当![]() 是偶数时,
是偶数时,![]() 是
是![]() 的偶数倍.
的偶数倍.
事实上,当![]() 时结论成立.假设
时结论成立.假设![]() 时成立,当
时成立,当![]() 时,由
时,由![]() 知,结论也成立.
知,结论也成立.
设![]() 的最小正周期是
的最小正周期是![]() ,因为
,因为![]() ,所以
,所以![]() 是偶数.
是偶数.
反过来,当![]() 是偶数时,我们证明存在一个以
是偶数时,我们证明存在一个以![]() 为最小正周期的“
为最小正周期的“![]() 一数列”
一数列”![]() .
.
事实上,令![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,之后再以
,之后再以![]() 为周期循环即可.
为周期循环即可.
当![]() 以
以![]() 为最小正周期时,集合
为最小正周期时,集合![]() 的元素个数为
的元素个数为![]() ,其中
,其中![]() 表示不超过
表示不超过![]() 的最大整数.因此所求即为
的最大整数.因此所求即为![]() ,
,![]() ,…,
,…,![]() 中不同项的个数.
中不同项的个数.
当![]() 时,
时,![]() ,所以从
,所以从![]() 到0中的所有整数值都能取到,有32种.
到0中的所有整数值都能取到,有32种.
当![]() 时,
时,![]() ,所以
,所以![]() ,
,![]() ,…,
,…,![]() 两两不同,有31种.
两两不同,有31种.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案【题目】随着科技的发展,网络已逐渐融入了人们的生活.网购是非常方便的购物方式,为了了解网购在我市的普及情况,某调查机构进行了有关网购的调查问卷,并从参与调查的市民中随机抽取了男女各100人进行分析,从而得到表(单位:人)
经常网购 | 偶尔或不用网购 | 合计 | |
男性 | 50 | 100 | |
女性 | 70 | 100 | |
合计 |
(1)完成上表,并根据以上数据判断能否在犯错误的概率不超过0.01的前提下认为我市市民网购与性别有关?
(2)①现从所抽取的女市民中利用分层抽样的方法抽取10人,再从这10人中随机选取3人赠送优惠券,求选取的3人中至少有2人经常网购的概率;
②将频率视为概率,从我市所有参与调查的市民中随机抽取10人赠送礼品,记其中经常网购的人数为![]() ,求随机变量
,求随机变量![]() 的数学期望和方差.
的数学期望和方差.
参考公式: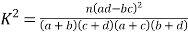
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

