题目内容
已知函数f(x)=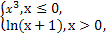 若f(2-x2)>f(x),则实数x的取值范围是( )
若f(2-x2)>f(x),则实数x的取值范围是( )
(A)(-∞,-1)∪(2,+∞)
(B)(-∞,-2)∪(1,+∞)
(C)(-1,2)
(D)(-2,1)
D
【解析】画出函数f(x)的大致图象如图,
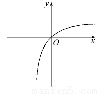
由图形易知f(x)在R上为单调递增函数,因此由f(2-x2)>f(x)可知2-x2>x,即x2+x-2<0,解得-2<x<1,即实数x的取值范围是(-2,1).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
已知函数f(x)=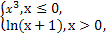 若f(2-x2)>f(x),则实数x的取值范围是( )
若f(2-x2)>f(x),则实数x的取值范围是( )
(A)(-∞,-1)∪(2,+∞)
(B)(-∞,-2)∪(1,+∞)
(C)(-1,2)
(D)(-2,1)
D
【解析】画出函数f(x)的大致图象如图,

由图形易知f(x)在R上为单调递增函数,因此由f(2-x2)>f(x)可知2-x2>x,即x2+x-2<0,解得-2<x<1,即实数x的取值范围是(-2,1).

 阅读快车系列答案
阅读快车系列答案