题目内容
【题目】双曲线E:![]() (
(![]() ,
,![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,
,![]() ,已知点
,已知点![]() 为抛物线C:
为抛物线C:![]() 的焦点,且到双曲线E的一条渐近线的距离为
的焦点,且到双曲线E的一条渐近线的距离为![]() ,又点P为双曲线E上一点,满足
,又点P为双曲线E上一点,满足![]() .则
.则
(1)双曲线的标准方程为______;
(2)![]() 的内切圆半径与外接圆半径之比为______.
的内切圆半径与外接圆半径之比为______.
【答案】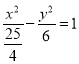
![]()
【解析】
根据抛物线方程可求得焦点坐标,由![]() 到其双曲线的渐近线的距离可求得
到其双曲线的渐近线的距离可求得![]() 再由双曲线中
再由双曲线中![]() 的关系即可求得双曲线标准方程;设点P在双曲线的右支上,
的关系即可求得双曲线标准方程;设点P在双曲线的右支上,![]() ,则
,则![]() ,根据余弦定理求得
,根据余弦定理求得![]() ,进而结合双曲线中焦点三角形面积公式求得内切圆半径,由正弦定理求得外接圆半径,即可求得
,进而结合双曲线中焦点三角形面积公式求得内切圆半径,由正弦定理求得外接圆半径,即可求得![]() 的内切圆半径与外接圆半径之比.
的内切圆半径与外接圆半径之比.
![]() 到其双曲线的渐近线的距离为
到其双曲线的渐近线的距离为![]() ,而抛物线
,而抛物线![]() 的焦点
的焦点![]() ,
,
![]() ,
,
则双曲线的标准方程为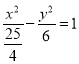 ;
;
设点P在双曲线的右支上,![]() ,则
,则![]() ,
,
则由余弦定理可得![]() ,
,
解得![]() ,
,![]() (舍去),
(舍去),
设![]() 的内切圆和外接圆的半径分别为r,R,
的内切圆和外接圆的半径分别为r,R,
![]() ,
,
解得![]() ,
,
而由正弦定理可得![]() ,
,
所以![]() .
.
故答案为: ;
;![]() .
.

练习册系列答案
相关题目
【题目】今年1月至2月由新型冠状病毒引起的肺炎病例陡然增多,为了严控疫情传播,做好重点人群的预防工作,某地区共统计返乡人员![]() 人,其中
人,其中![]() 岁及以上的共有
岁及以上的共有![]() 人.这
人.这![]() 人中确诊的有
人中确诊的有![]() 名,其中
名,其中![]() 岁以下的人占
岁以下的人占![]() .
.
(1)请将下面的列联表补充完整,并判断是否有![]() %的把握认为是否确诊患新冠肺炎与年龄有关;
%的把握认为是否确诊患新冠肺炎与年龄有关;
确诊患新冠肺炎 | 未确诊患新冠肺炎 | 合计 | |
50岁及以上 | 40 | ||
50岁以下 | |||
合计 | 10 | 100 |
(2)为了研究新型冠状病毒的传染源和传播方式,从![]() 名确诊人员中随机抽出
名确诊人员中随机抽出![]() 人继续进行血清的研究,
人继续进行血清的研究,![]() 表示被抽取的
表示被抽取的![]() 人中
人中![]() 岁以下的人数,求
岁以下的人数,求![]() 的分布列以及数学期望.
的分布列以及数学期望.
参考表:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
参考公式: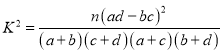 ,其中
,其中![]() .
.
