题目内容
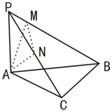 20、直角三角形ABC中∠C=90°,PA⊥平面ABC,AM⊥PB于M,AN⊥PC于N.
20、直角三角形ABC中∠C=90°,PA⊥平面ABC,AM⊥PB于M,AN⊥PC于N.求证:①BC⊥平面PAC;
②PB⊥平面AMN.
分析:①由已知中直角三角形ABC中∠C=90°,PA⊥平面ABC,我们易得到AC⊥BC,PA⊥BC,由线面垂直的判定定理,即可得到BC⊥平面PAC;
②由①的结论,结合线面垂直的性质,可得BC⊥AN,由AM⊥PB于M,AN⊥PC于N,我们由线面垂直的判定定理,即可得到PB⊥平面AMN.
②由①的结论,结合线面垂直的性质,可得BC⊥AN,由AM⊥PB于M,AN⊥PC于N,我们由线面垂直的判定定理,即可得到PB⊥平面AMN.
解答:证明:①∵直角三角形ABC中∠C=90°,
∴AC⊥BC
又∵PA⊥平面ABC,
∴PA⊥BC
又由PA∩AC=A
∴BC⊥平面PAC;
②由①中结论得:BC⊥AN
又∵AN⊥PC于N.BC∩PC=C
∴AN⊥平面PBC,又由PB?平面PBC,
∴AN⊥PB,又由AM⊥PB于M,AN∩AM=A
∴PB⊥平面AMN
∴AC⊥BC
又∵PA⊥平面ABC,
∴PA⊥BC
又由PA∩AC=A
∴BC⊥平面PAC;
②由①中结论得:BC⊥AN
又∵AN⊥PC于N.BC∩PC=C
∴AN⊥平面PBC,又由PB?平面PBC,
∴AN⊥PB,又由AM⊥PB于M,AN∩AM=A
∴PB⊥平面AMN
点评:本题考查的知识点是直线与平面垂直的判定,熟练掌握空间中直线与平面垂直的判定定理,是解答本题的关键.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
 15、(选做题)(几何证明选讲选做题)如图,直角三角形ABC中,∠B=90°,AB=4,以BC为直径的圆交AC边于点D,AD=2,则∠C的大小为
15、(选做题)(几何证明选讲选做题)如图,直角三角形ABC中,∠B=90°,AB=4,以BC为直径的圆交AC边于点D,AD=2,则∠C的大小为 (2012•宝鸡模拟)如图,已知PA⊥平面ABC,且
(2012•宝鸡模拟)如图,已知PA⊥平面ABC,且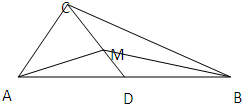 如图:直角三角形ABC中,AC⊥BC,AB=2,D是AB的中点,M是CD上的动点.
如图:直角三角形ABC中,AC⊥BC,AB=2,D是AB的中点,M是CD上的动点.