题目内容
已知函数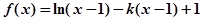 .
.
(1)求函数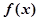 的单调区间; (2)若
的单调区间; (2)若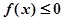 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;
(3)证明: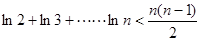

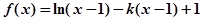 .
.(1)求函数
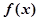 的单调区间; (2)若
的单调区间; (2)若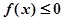 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;(3)证明:
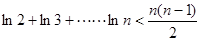

(1)当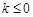 时,函数
时,函数 的递增区间为
的递增区间为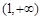 ,;当
,;当 时,函数
时,函数 的递增区间为
的递增区间为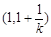 ,递减区间为
,递减区间为 ; (2)
; (2)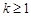 (3)证明如下
(3)证明如下
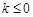 时,函数
时,函数 的递增区间为
的递增区间为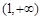 ,;当
,;当 时,函数
时,函数 的递增区间为
的递增区间为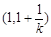 ,递减区间为
,递减区间为 ; (2)
; (2)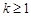 (3)证明如下
(3)证明如下试题分析:解:(1)
 的定义域为
的定义域为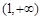 ,
,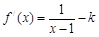
当
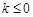 时,函数
时,函数 的递增区间为
的递增区间为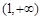 ,
,当
 时,函数
时,函数 的递增区间为
的递增区间为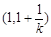 ,递减区间为
,递减区间为 ;
;(2)由
 得,
得,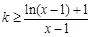 ,
,令
 ,则
,则 ,
,∴当
 时,
时,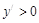 函数递增;当
函数递增;当 时,
时, 函数递减。
函数递减。∴当
 时函数取得最大值为1,∴
时函数取得最大值为1,∴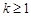 ,
,(3)由(1)可知若
 ,当
,当 时有
时有
 ,即
,即 ,即有
,即有 (x>1),
(x>1), 令
 ,则
,则 ,
,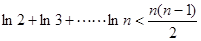 ,
, 点评:导数常应用于求曲线的切线方程、求函数的最值与单调区间、证明不等式和解不等式中参数的取值范围等。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的图象如图所示,将
的图象如图所示,将 的图象向左平移
的图象向左平移 个单位,得到
个单位,得到 的图象,则函数
的图象,则函数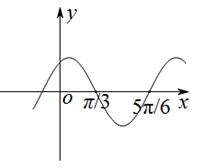


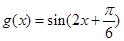
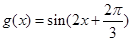
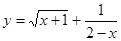 的定义域是 。
的定义域是 。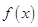 是R上的奇函数,若对于
是R上的奇函数,若对于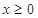 ,都有
,都有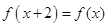 ,
,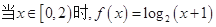 时,
时,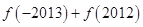 的值为( )
的值为( )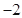
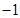
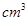 ,高为2
,高为2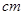 长方体的无盖铁盒,问这个铁盒底面的长和宽各为多少时材料最省?
长方体的无盖铁盒,问这个铁盒底面的长和宽各为多少时材料最省? 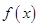 满足
满足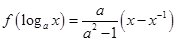 ,其中a>0,a≠1.
,其中a>0,a≠1.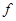
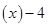 的值为负数,求
的值为负数,求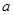 的取值范围。
的取值范围。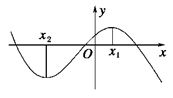
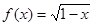 定义域为
定义域为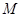 ,
,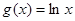 定义域为
定义域为 ,则
,则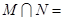 ( )
( )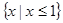
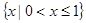
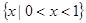

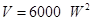 ,若把一颗钻石切割成1︰3的两颗钻石,则价值损失的百分率为( )(价值损失百分率
,若把一颗钻石切割成1︰3的两颗钻石,则价值损失的百分率为( )(价值损失百分率 ,切割中重量损耗不计)
,切割中重量损耗不计)