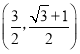题目内容
【题目】已知自变量为![]() 的函数
的函数![]() .其中
.其中![]() ,
,![]() 为自然对数的底,
为自然对数的底,![]() .
.
(Ⅰ)求函数![]() 与
与![]() 的单调区间,并且讨论函数
的单调区间,并且讨论函数![]() 的单调性;
的单调性;
(Ⅱ)已知![]() ,求证:
,求证:
(ⅰ)方程![]() 有两个根
有两个根![]() ,
,![]() ;
;
(ⅱ)若(ⅰ)中的两个根满足![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
【答案】(Ⅰ)![]() 增区间为
增区间为![]() ,减区间为
,减区间为![]() ;
;![]() 增区间为
增区间为![]() ,见解析(Ⅱ)(ⅰ)见解析(ⅱ)见解析
,见解析(Ⅱ)(ⅰ)见解析(ⅱ)见解析
【解析】
(Ⅰ)分别求得![]() ,
,![]() 的导数,由导数大于0,可得增区间;导数小于0,可得减区间,进而得到最值,可得单调区间;讨论
的导数,由导数大于0,可得增区间;导数小于0,可得减区间,进而得到最值,可得单调区间;讨论![]() 为奇数和偶数,即可得到所求单调性;
为奇数和偶数,即可得到所求单调性;
(Ⅱ)![]() ,(ⅰ)运用
,(ⅰ)运用![]() 为奇数的函数的单调性,结合图象即可得证;
为奇数的函数的单调性,结合图象即可得证;
(ⅱ)![]() 为奇数时,
为奇数时,![]() 在
在![]() 递减,在
递减,在![]() 递增,且
递增,且![]() 越小,函数的图象与直线
越小,函数的图象与直线![]() 的交点越靠近
的交点越靠近![]() 轴,即可得证.
轴,即可得证.
解:(Ⅰ)![]() 的导数为
的导数为
![]() ,由
,由![]() 时
时![]() ;由
;由![]() 时
时![]() ;
;
可得![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() ;
;
![]() 的导数为
的导数为
![]() ,
,![]() ,
,
可得![]() ,
,
可得![]() 的增区间为
的增区间为![]() ;
;
![]() 经过
经过![]() 次导数可得
次导数可得![]() ,
,
由![]() ,在
,在![]() 时,
时,![]() ;
;![]() 时
时![]() ;
;
则![]() 次求导时,导函数在
次求导时,导函数在![]() 递增;
递增;![]() 递减,
递减,
即有导函数的最小值为0,
可得![]() 为奇数,
为奇数,![]() 在
在![]() 递减,在
递减,在![]() 递增;
递增;
![]() 为偶数时,
为偶数时,![]() 在
在![]() 递增;
递增;
(Ⅱ)证明:![]() ,(ⅰ)由
,(ⅰ)由![]() 为奇数,
为奇数,![]() 在
在![]() 递减,
递减,
在![]() 递增;可得
递增;可得![]() ,有最小值0,无最大值,
,有最小值0,无最大值,
则方程![]() 有两个根
有两个根![]() ,
,![]() ;
;
(ⅱ)若(ⅰ)中的两个根满足![]() ,
,![]() ,
,
由于![]() 为奇数时,
为奇数时,![]() 在
在![]() 递减,在
递减,在![]() 递增,
递增,
且![]() 越小,函数的图象与直线
越小,函数的图象与直线![]() 的交点越靠近
的交点越靠近![]() 轴,
轴,
则![]() ,
,![]() .
.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目