题目内容
【题目】已知椭圆![]() 的离心率是
的离心率是![]() ,点
,点![]() 在椭圆上,A,B分别为椭圆的右顶点与上顶点,过点A,B引椭圆C的两条弦AE、BF交椭圆于点E,F.
在椭圆上,A,B分别为椭圆的右顶点与上顶点,过点A,B引椭圆C的两条弦AE、BF交椭圆于点E,F.
![]() 求椭圆C的方程;
求椭圆C的方程;
![]() 若直线AE,BF的斜率互为相反数,
若直线AE,BF的斜率互为相反数,
![]() 求出直线EF的斜率;
求出直线EF的斜率;
![]() 若O为直角坐标原点,求
若O为直角坐标原点,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)直线EF的斜率
;(2)直线EF的斜率![]() ,
,![]() 面积的最大值
面积的最大值![]() .
.
【解析】
![]() 根据椭圆的离心率公式,将点代入椭圆方程,即可求得a和b的值,求得椭圆方程;
根据椭圆的离心率公式,将点代入椭圆方程,即可求得a和b的值,求得椭圆方程;
![]() 设直线AE及BF的方程,代入椭圆方程,求得E和F点坐标,根据直线的斜率公式,即可直线EF的斜率;
设直线AE及BF的方程,代入椭圆方程,求得E和F点坐标,根据直线的斜率公式,即可直线EF的斜率;
![]() 设直线EF的方程,代入椭圆方程,利用韦达定理及弦长公式求得
设直线EF的方程,代入椭圆方程,利用韦达定理及弦长公式求得![]() ,根据三角形的面积公式及二次函数的性质,即可求得答案.
,根据三角形的面积公式及二次函数的性质,即可求得答案.
解:![]() 由椭圆的离心率
由椭圆的离心率![]() ,
,
则![]() ,将点代入椭圆方程:
,将点代入椭圆方程:![]() ,
,
解得![]() ,
,![]() ,
,
![]() 椭圆的标准方程:
椭圆的标准方程:![]() ;
;
![]() 设
设![]() ,
,![]() ,直线AE的方程:
,直线AE的方程:![]() ,
,
联立![]() ,整理得:
,整理得:![]() ,
,
解得:![]() ,或
,或 ,
,
![]() ,
,
设直线BF的方程为:![]() ,联立
,联立![]() ,
,
整理得:![]() ,解得:
,解得:![]() 或
或 ,
,
![]() ,则直线EF的斜率
,则直线EF的斜率![]() ,
,
![]() 直线EF的斜率
直线EF的斜率![]() ;
;
![]() 设直线EF的方程:
设直线EF的方程:![]() ,
,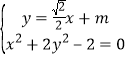 ,
,
整理得:![]() ,
,
![]() ,则
,则![]() ,
,
则![]() ,
,![]() ,
,
![]() ,
,
O到直线EF的距离![]() ,则
,则![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,
![]() 时,
时,![]() 取最大值,最大值为
取最大值,最大值为![]() ,
,
![]() 面积的最大值
面积的最大值![]() .
.

练习册系列答案
相关题目
【题目】北京市环境保护监测中心每月向公众公布北京市各区域的空气质量状况![]() 年1月份各区域的
年1月份各区域的![]() 浓度情况如表:
浓度情况如表:
各区域1月份![]() 浓度
浓度![]() 单位:微克
单位:微克![]() 立方米
立方米![]() 表
表
区域 |
| 区域 |
| 区域 |
|
怀柔 | 27 | 海淀 | 34 | 平谷 | 40 |
密云 | 31 | 延庆 | 35 | 丰台 | 42 |
门头沟 | 32 | 西城 | 35 | 大兴 | 46 |
顺义 | 32 | 东城 | 36 | 开发区 | 46 |
昌平 | 32 | 石景山 | 37 | 房山 | 47 |
朝阳 | 34 | 通州 | 39 |
从上述表格随机选择一个区域,其2018年1月份![]() 的浓度小于36微克
的浓度小于36微克![]() 立方米的概率是
立方米的概率是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()

