题目内容
18．函数y=$\frac{{x}^{2}-3x+3}{x-1}$（x＞1）的值域为[1，+∞）．分析 根据分式的性质结合基本不等式进行求解即可．
解答 解：令t=x-1，∵x＞1，∴t＞0，
则x=t+1，
则y=$\frac{{x}^{2}-3x+3}{x-1}$=$\frac{（t+1）^{2}-3（t+1）+3}{t}$=$\frac{{t}^{2}-t+1}{t}$=t+$\frac{1}{t}$-1，
∵t＞0，
∴t+$\frac{1}{t}$-1$≥2\sqrt{t•\frac{1}{t}}$-1=2-1=1，
当且仅当t=$\frac{1}{t}$，即t=1时，取等号，
故函数y的最小值为1，
即函数的值域为[1，+∞），
故答案为：[1，+∞）
点评 本题主要考查函数值域的求解，利用换元法结合基本不等式的应用是解决本题的关键．
练习册系列答案
相关题目
6．如果y=f（x）的反函数是y=f-1（x），则下列命题中一定正确的是（ ）
| A． | 若y=f（x）在[1，2]上是增函数，则y=f-1（x）在[1，2]上也是增函数 | |
| B． | 若y=f（x）是奇函数，则y=f-1（x）也是奇函数 | |
| C． | 若y=f（x）是偶函数，则y=f-1（x）也是偶函数 | |
| D． | 若y=f（x）的图象与y轴有交点，则y=f-1（x）的图象与y轴也有交点 |
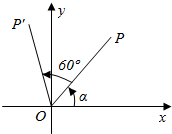如图，保持点P（3，3）与原点的距离不变，并绕原点旋转60°到P′位置，设点P′的坐标为（x′，y′）．