题目内容
有下列命题:
①设集合M = {x | 0< x ≤3},N = {x | 0< x ≤2},则“a∈M”是“a∈N”的充分而不必要条件;
②命题“若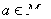 ,则
,则 ”的逆否命题是:若
”的逆否命题是:若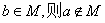 ;
;
③若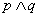 是假命题,则
是假命题,则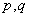 都是假命题;
都是假命题;
④命题P:“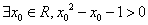 ”的否定
”的否定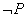 :“
:“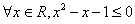 ”
”
则上述命题中为真命题的是
| A.①②③④ | B.①③④ | C.②④ | D.②③④ |
C
解析试题分析:对于①设集合M = {x | 0< x ≤3},N = {x | 0< x ≤2},则“a∈M”是“a∈N”的充分而不必要条件;根据大集合是小集合成立的必要不充分条件可知错误。
②命题“若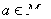 ,则
,则 ”的逆否命题是:若
”的逆否命题是:若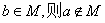 ;成立
;成立
③若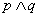 是假命题,则
是假命题,则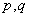 都是假命题;因为且命题一假即假,因此不成立。
都是假命题;因为且命题一假即假,因此不成立。
④命题P:“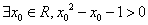 ”的否定
”的否定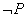 :“
:“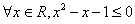 成立,故选C.
成立,故选C.
考点:命题的真值
点评:此种题型往往比较综合考查多个知识点的概念,处理的关键是熟练掌握各个知识点的概念、定义.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
若命题 ,则
,则 :( )
:( )
A. | B. |
C. | D.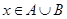 |
下列选项叙述错误的是( )
| A.命题“若x≠l,则x2-3x十2≠0”的逆否命题是“若x2-3x十2=0,则x=1” |
B.若命题p: x x R,x2+x十1≠0,则 R,x2+x十1≠0,则 p: p: R,x2+x十1=0 R,x2+x十1=0 |
C.若p q为真命题,则p,q均为真命题 q为真命题,则p,q均为真命题 |
| D.“x>2”是“x2一3x+2>0”的充分不必要条件 |
下列关于命题的说法中错误的是( )
A.对于命题P: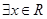 ,使得 ,使得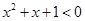 ,则 ,则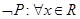 ,则 ,则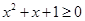 |
B.“ ”是“ ”是“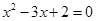 ”的充分不必要条件 ”的充分不必要条件 |
C.命题“若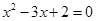 ,则 ,则 ”的逆否命题是:“若 ”的逆否命题是:“若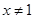 ,则 ,则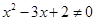 ” ” |
D.若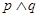 为假命题,则 为假命题,则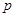 、 、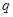 均为假命题 均为假命题 |
“函数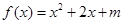 存在零点”的一个必要不充分条件是( )
存在零点”的一个必要不充分条件是( )
A.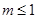 | B.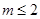 | C.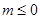 | D.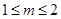 |
已知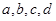 是实数,则“
是实数,则“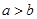 且
且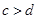 ”是“
”是“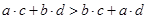 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
给出下面结论:
(1)命题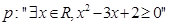 的否定为
的否定为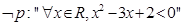 ;
;
(2)若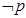 是
是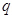 的必要不充分条件,则
的必要不充分条件,则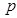 是
是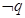 的充分不必要条件;
的充分不必要条件;
(3)“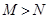 ”是“
”是“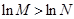 ”成立的充分不必要条件;
”成立的充分不必要条件;
(4) 若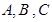 是
是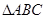 的三个内角,则“
的三个内角,则“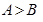 ”是“
”是“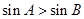 ”成立的充要条件。
”成立的充要条件。
其中正确结论的个数是
| A.4 | B.3 | C.2 | D.1 |
已知三个命题:①方程x2-x+2=0的判别式小于或等于零;②若|x|≥0,则x≥0;③5>2且3<7.其中真命题是
| A.①和② | B.①和③ | C.②和③ | D.只有① |
 ,使得
,使得 ”的否定是“
”的否定是“ ,都有
,都有 ”.
”. 中,F为右焦点,
中,F为右焦点, 为左顶点,点
为左顶点,点 且
且
 ,则此双曲线的离心率为
,则此双曲线的离心率为 .
. 是夹角为
是夹角为 的单位向量,则向量
的单位向量,则向量 与
与 垂直的充要条件是
垂直的充要条件是 .
.