题目内容
【题目】如图,矩形CDEF和梯形ABCD互相垂直,![]() ,
,![]() ,
,![]() .
.
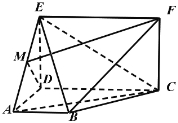
(1)若![]() 为
为![]() 中点,求证:
中点,求证:![]() ∥平面
∥平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的大小.
所成锐二面角的大小.
【答案】(1)证明见解析(2)![]()
【解析】
(1)设![]() 与
与![]() 交于点
交于点![]() ,连结
,连结![]() ,在矩形
,在矩形![]() 中,点
中,点![]() 为
为![]() 中点,求证
中点,求证![]() ∥
∥![]() ,即可求得答案;
,即可求得答案;
(2)以![]() 为坐标原点, 其中
为坐标原点, 其中![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
求出平面![]() 的法向量
的法向量![]() 和平面
和平面![]() 的法向量
的法向量![]() ,根据
,根据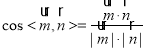 ,即可求得答案.
,即可求得答案.
(1)设![]() 与
与![]() 交于点
交于点![]() ,连结
,连结![]() ,在矩形
,在矩形![]() 中,点
中,点![]() 为
为![]() 中点,
中点,
如图:
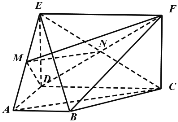
![]()
![]() 为
为![]() 中点,
中点,
![]()
![]() ∥
∥![]()
又![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]()
![]() ∥平面
∥平面![]() .
.
(2)![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,
![]()
![]() 平面
平面![]() ,
,
以![]() 为坐标原点, 其中
为坐标原点, 其中![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
如图:
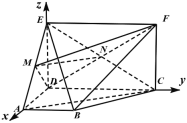
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
可得:![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
由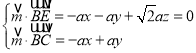
可得![]() 得到
得到![]() 的一个解为
的一个解为![]() ,
,
注意到平面![]() 的法向量
的法向量![]() ,
,
而![]() ,
,
![]() 平面
平面![]() 与
与![]() 所成锐二面角的大小为
所成锐二面角的大小为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.在购进机器时,可以一次性额外购买几次维修服务,每次维修服务费用200元,另外实际维修一次还需向维修人员支付小费,小费每次50元.在机器使用期间,如果维修次数超过购机时购买的维修服务次数,则每维修一次需支付维修服务费用500元,无需支付小费.现需决策在购买机器时应同时一次性购买几次维修服务,为此搜集并整理了100台这种机器在三年使用期内的维修次数,得下面统计表:
维修次数 | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 20 | 30 | 30 | 10 |
记x表示1台机器在三年使用期内的维修次数,y表示1台机器在维修上所需的费用(单位:元),![]() 表示购机的同时购买的维修服务次数.
表示购机的同时购买的维修服务次数.
(1)若![]() =10,求y与x的函数解析式;
=10,求y与x的函数解析式;
(2)若要求“维修次数不大于![]() ”的频率不小于0.8,求n的最小值;
”的频率不小于0.8,求n的最小值;
(3)假设这100台机器在购机的同时每台都购买10次维修服务,或每台都购买11次维修服务,分别计算这100台机器在维修上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买10次还是11次维修服务?