题目内容
已知三点O(0,0),A(-2,1),B(2,1),曲线C上任意一点M(x,y)满足| +
+ |=
|= ·(
·( +
+ )+2.
)+2.
(1)求曲线C的方程;
(2)点Q(x0,y0)(-2<x0<2)是曲线C上的动点,曲线C在点Q处的切线为 ,点P的坐标是(0,-1),
,点P的坐标是(0,-1), 与PA,PB分别交于点D,E,求△QAB与△PDE的面积之比.
与PA,PB分别交于点D,E,求△QAB与△PDE的面积之比.
(1)曲线C的方程是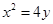 ;(2)△QAB与△PDE的面积之比
;(2)△QAB与△PDE的面积之比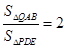 .
.
解析试题分析:(1)将向量式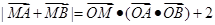 化为坐标式,即可得曲线C的方程是
化为坐标式,即可得曲线C的方程是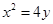 .(2)
.(2)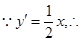 曲线C在Q处的切线
曲线C在Q处的切线 的方程是
的方程是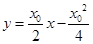 , 且与y轴的交点为
, 且与y轴的交点为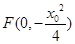 ,
,
再联立直线PA,PB与曲线C的方程,得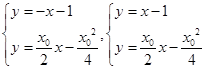 ,
,
利用韦达定理计算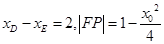 ,由三角形的面积公式有
,由三角形的面积公式有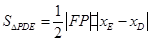 ,因为
,因为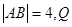 到
到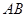 的距离为
的距离为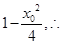
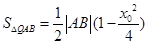 ,则
,则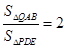 .
.
试题解析:解:(1)由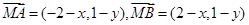 ,
,
得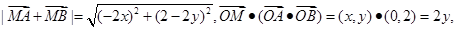
由已知得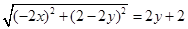 , 化简得曲线C的方程是
, 化简得曲线C的方程是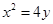 .
.
(2)直线PA,PB的方程分别是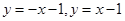 , 曲线C在Q处的切线l的方程是
, 曲线C在Q处的切线l的方程是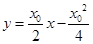 , 且与y轴的交点为
, 且与y轴的交点为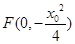 ,
,
分别联立方程,得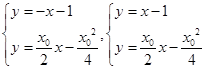 ,
,
解得D,E的横坐标分别是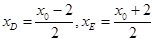 , 则
, 则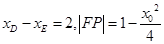 ,
,
故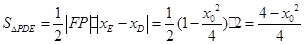 ,
,
而 ,则
,则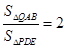 .
.
即△QAB与△PDE的面积之比为2.
考点:1、向量的坐标式、向量的模、数量积的坐标运算;2、曲线的切线方程;3、韦达定理;4、三角形的面积公式及三角形面积的分割求法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 =3
=3 ,
, =2
=2 ,求点M、N及
,求点M、N及 的坐标.
的坐标.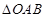 中,已知
中,已知 为线段
为线段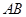 上的一点,
上的一点,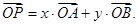
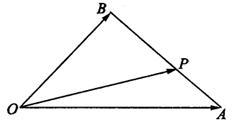
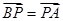 ,求
,求 ,
, 的值;
的值;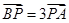 ,
,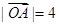 ,
,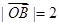 ,且
,且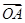 与
与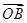 的夹角为60°时,求
的夹角为60°时,求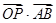 的值。
的值。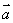 =(
=(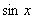 ,1),
,1),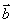 =(
=(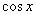 ,1),
,1),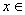 R.
R.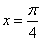 时,求向量
时,求向量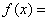 |
|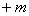 为奇函数,求实数
为奇函数,求实数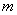 的值.
的值.
 ;
; ,求实数
,求实数 的值。
的值。 、
、 、
、 两两所成的角相等,并且|
两两所成的角相等,并且| )·
)· =0,求t的值。
=0,求t的值。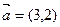 ,
,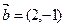 ,若
,若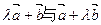 平行,则λ= .
平行,则λ= .