题目内容
正四棱柱ABCD-A′B′C′D′各顶点都在表面积为24π的球面上,且底边AB的长为2,则顶点A到平面A'BD的距离为分析:先设出球的半径为R,根据求表面积公式求出R,并且求出AA′.
方法一三棱锥A-ABD的体积的两种算法:一种算法以A为顶点,则A到平面A′BD的距离设为h,算出体积;另一种以A′为顶点,则A′到平面ABD的距离为AA′,算出体积.相等得到答案.
方法二找出BD中点O,连接A′O过A作AH⊥A′O,垂足为H,由平面AA′O⊥平面A′BD,得到AH⊥平面A′BD,即AH为点A到平面A'BD的距离.利用三角形的面积法求出AH即可.
方法一三棱锥A-ABD的体积的两种算法:一种算法以A为顶点,则A到平面A′BD的距离设为h,算出体积;另一种以A′为顶点,则A′到平面ABD的距离为AA′,算出体积.相等得到答案.
方法二找出BD中点O,连接A′O过A作AH⊥A′O,垂足为H,由平面AA′O⊥平面A′BD,得到AH⊥平面A′BD,即AH为点A到平面A'BD的距离.利用三角形的面积法求出AH即可.
解答: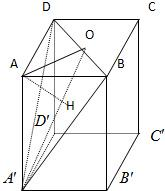 解:设球半径为R,则S表=4πR2=24π,则R2=6,
解:设球半径为R,则S表=4πR2=24π,则R2=6,
由AC'=2R,
即A'A2+AB2+AD2=(2R)2,
得AA'=4.
法一等体积法,利用VA'-ABD=VA-A'BD.设点A到平面A'BD的距离为h,设O为BD
中点,连A′O,则A′O⊥BD,
易得A′O=
,BD=2
.
由VA′-ABD=
•AA′•
AB•AD=
,VA-A′BD=
h•S△A′BD,
易求S△A′BD=
BD•A′O=6,
所以
=
h•6?h=
.
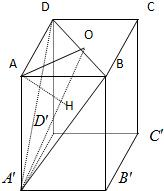 法二过A作AH⊥A′O,垂足为H,
法二过A作AH⊥A′O,垂足为H,
∵平面AA′O⊥平面A′BD,
∴AH⊥平面A′BD,即AH为点A到平面A'BD的距离.
在RT△A′BD中,AA′•AO=AH•A′O,
即4•
=
h,得h=
;
故答案是
.
 解:设球半径为R,则S表=4πR2=24π,则R2=6,
解:设球半径为R,则S表=4πR2=24π,则R2=6,由AC'=2R,
即A'A2+AB2+AD2=(2R)2,
得AA'=4.
法一等体积法,利用VA'-ABD=VA-A'BD.设点A到平面A'BD的距离为h,设O为BD
中点,连A′O,则A′O⊥BD,
易得A′O=
| 18 |
| 2 |
由VA′-ABD=
| 1 |
| 3 |
| 1 |
| 2 |
| 8 |
| 3 |
| 1 |
| 3 |
易求S△A′BD=
| 1 |
| 2 |
所以
| 8 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
 法二过A作AH⊥A′O,垂足为H,
法二过A作AH⊥A′O,垂足为H,∵平面AA′O⊥平面A′BD,
∴AH⊥平面A′BD,即AH为点A到平面A'BD的距离.
在RT△A′BD中,AA′•AO=AH•A′O,
即4•
| 2 |
| 18 |
| 4 |
| 3 |
故答案是
| 4 |
| 3 |
点评:在解决多面体与球有关接、切问题时,一般做出一个适当截面,将其转化为平面问题解决.这类截面通常是球的大圆、多面体的对角面等,在这个截面中应包括每个几何体的主要元素,并且能反映出体与体之间的主要位置关系和数量关系.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
顶点在同一球面上的正四棱柱ABCD-A′B′C′D′中,AB=1,AA′=
,则A、C两点间的球面距离为( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=
如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=| 3 |
| 2 |
| A、30° | B、45° |
| C、60° | D、90° |
 如图(1),正四棱柱ABCD-A′B′C′D′中,AA′=2AB,则异面直线A′B与AD′所成的角的余弦值是
如图(1),正四棱柱ABCD-A′B′C′D′中,AA′=2AB,则异面直线A′B与AD′所成的角的余弦值是