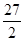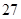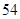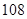题目内容
已知数列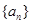 的前
的前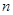 项和为
项和为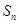 ,常数
,常数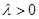 ,且
,且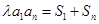 对一切正整数
对一切正整数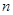 都成立。
都成立。
(Ⅰ)求数列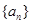 的通项公式;
的通项公式;
(Ⅱ)设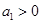 ,
,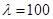 ,当
,当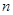 为何值时,数列
为何值时,数列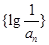 的前
的前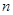 项和最大?
项和最大?
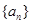 的前
的前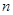 项和为
项和为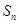 ,常数
,常数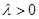 ,且
,且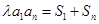 对一切正整数
对一切正整数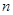 都成立。
都成立。(Ⅰ)求数列
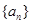 的通项公式;
的通项公式;(Ⅱ)设
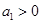 ,
,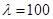 ,当
,当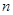 为何值时,数列
为何值时,数列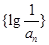 的前
的前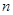 项和最大?
项和最大?(Ⅰ)当 ;(Ⅱ)数列
;(Ⅱ)数列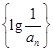 的前六项和最大.
的前六项和最大.
 ;(Ⅱ)数列
;(Ⅱ)数列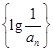 的前六项和最大.
的前六项和最大.试题分析:(Ⅰ)令
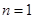 可得
可得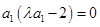 ,在此要对
,在此要对 的值进行讨论,当
的值进行讨论,当 时,
时,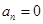 ;当
;当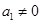 时,消去
时,消去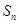 即可解出
即可解出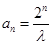 ;(Ⅱ)将
;(Ⅱ)将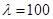 代入
代入 得到
得到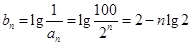 ,然后可以判断出
,然后可以判断出 是等差数列,然后判断出正负转折的项
是等差数列,然后判断出正负转折的项 ,
,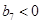 ,故前六项和最大.
,故前六项和最大.试题解析:(Ⅰ)取
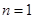 ,得
,得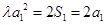 ,
,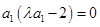 .
.若
 ,则
,则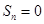 .当
.当 时,
时,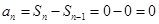 ,所以
,所以 .
.若
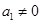 ,则
,则 .当
.当 时,
时, ,
,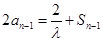 .
.两式相减得
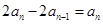 ,从而数列
,从而数列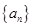 是等比数列,所以
是等比数列,所以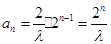 .
.综上所述,当
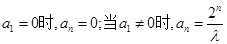 .
.(Ⅱ)当
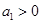 且
且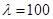 时,令
时,令 ,由(1)有
,由(1)有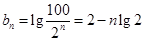 .
.所以数列
 是单调递减的等差数列(公差为
是单调递减的等差数列(公差为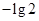 ).
). ,
,当
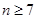 时,
时, ,
,故数列
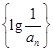 的前六项和最大.
的前六项和最大. 
练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
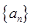 是各项都为正数的等比数列,
是各项都为正数的等比数列,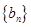 是等差数列,且
是等差数列,且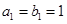 ,
,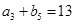 ,
,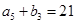 .
.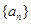 ,
,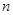 项和为
项和为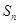 ,求数列
,求数列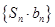 的前
的前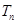 .
.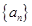 中,
中,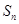 为其前n项和,若
为其前n项和,若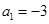 ,
,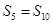 ,则当
,则当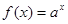 (
(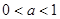 ),数列
),数列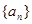 满足
满足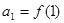 ,
,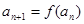 ,
,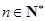 .则
.则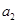 与
与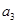 中,较大的是________;
中,较大的是________;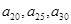 的大小关系是_____________.
的大小关系是_____________.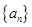 的通项公式
的通项公式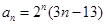 ,则数列的前
,则数列的前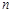 项和
项和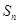 的最小值是( )
的最小值是( )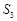
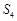
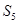
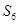
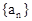 中,已知前15项的和
中,已知前15项的和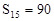 ,则
,则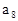 等于( )
等于( )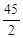
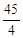
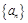 为等差数列,且
为等差数列,且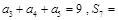 .
.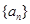 中,若
中,若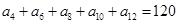 ,则
,则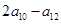 的值为( )
的值为( )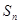 为等差数列
为等差数列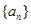 的前
的前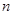 项和,
项和,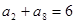 ,则
,则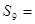 ( )
( )