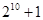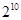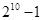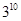题目内容
设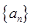 是各项都为正数的等比数列,
是各项都为正数的等比数列,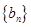 是等差数列,且
是等差数列,且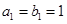 ,
,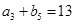 ,
,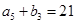 .
.
(1)求数列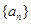 ,
,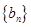 的通项公式;
的通项公式;
(2)设数列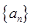 的前
的前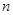 项和为
项和为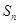 ,求数列
,求数列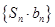 的前
的前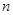 项和
项和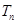 .
.
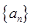 是各项都为正数的等比数列,
是各项都为正数的等比数列,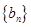 是等差数列,且
是等差数列,且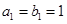 ,
,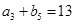 ,
,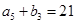 .
.(1)求数列
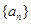 ,
,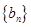 的通项公式;
的通项公式;(2)设数列
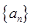 的前
的前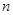 项和为
项和为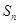 ,求数列
,求数列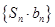 的前
的前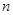 项和
项和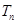 .
.(1)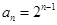 ,
,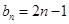 ;(2)
;(2)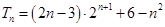 .
.
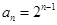 ,
,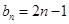 ;(2)
;(2)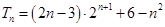 .
.试题分析:(1)在
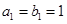 已知的条件下,利用等比数列
已知的条件下,利用等比数列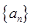 的公比
的公比 和等差数列
和等差数列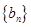 的公差
的公差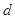 构建二元方程组,求解出
构建二元方程组,求解出 和
和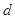 ,然后再利用等差数列和等比数列的通项公式得到数列
,然后再利用等差数列和等比数列的通项公式得到数列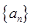 和
和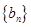 的通项公式;
的通项公式;(2)先利用等比数列的求和公式求出数列
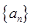 的前
的前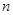 项和
项和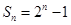 ,从而得到数列
,从而得到数列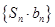 的通项公式
的通项公式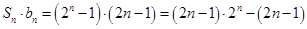 ,从而利用分组求和法分别求出数列
,从而利用分组求和法分别求出数列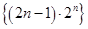 的前
的前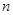 项和和数列
项和和数列 的前
的前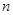 项和,再将两个前
项和,再将两个前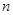 项和相减,在求数列
项和相减,在求数列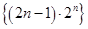 的前
的前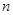 项和时,利用错位相减法,求数列
项和时,利用错位相减法,求数列 的前
的前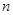 项和时,直接利用等差数列的求和公式即可.
项和时,直接利用等差数列的求和公式即可.试题解析:(1)设数列
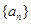 的公比为
的公比为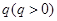 ,数列
,数列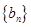 的公差为
的公差为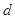 ,
,依题意得:
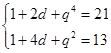 , 2分
, 2分消去
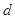 得
得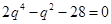
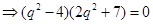 , 3分
, 3分∵
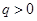 ∴
∴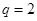 ,由
,由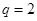 可解得
可解得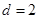 4分
4分∴
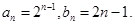 5分
5分(2)由(1)得
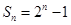 ,所以有:
,所以有: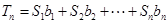
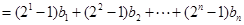
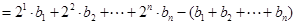 7分
7分令
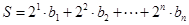 ① 则
① 则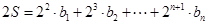 ②
②①-②得:
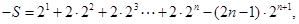 10分
10分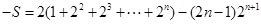
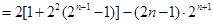
∴
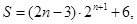 12分
12分又
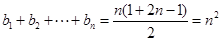 , 13分
, 13分∴
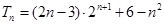 . 14分
. 14分
练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
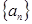 的前
的前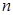 项和
项和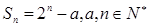 .设公差不为零的等差数列
.设公差不为零的等差数列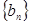 满足:
满足: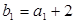 ,且
,且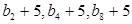 成等比.
成等比.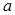 及
及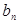 ;
;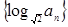 的前
的前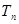 .求使
.求使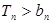 的最小正整数
的最小正整数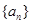 的前
的前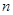 项和为
项和为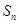 ,常数
,常数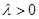 ,且
,且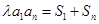 对一切正整数
对一切正整数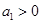 ,
,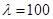 ,当
,当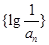 的前
的前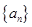 和等比数列
和等比数列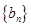 中,a1=2, 2b1=2, b6=32,
中,a1=2, 2b1=2, b6=32, 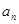 和
和 ;
;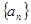 中,
中,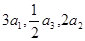 成等差数列,则
成等差数列,则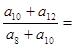 ( )
( )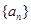 的前n项和为
的前n项和为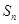 ,若
,若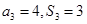 ,则公差
,则公差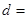 ___________.
___________.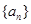 公比为
公比为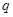 ,其前
,其前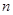 项和为
项和为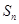 ,若
,若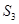 、
、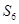 、
、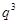 等于( )
等于( )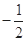
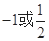
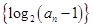
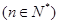 为等差数列,且
为等差数列,且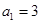 ,
,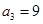 ,
,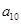 的值为( )
的值为( )