题目内容
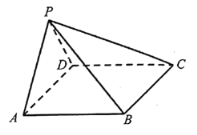
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为菱形,平面
为菱形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)当直线![]() 与平面
与平面![]() 所成角为
所成角为![]() 时,求二面角
时,求二面角![]() 平面角的大小.
平面角的大小.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,推导出
,推导出![]() ,
,![]() ,可证得直线
,可证得直线![]() 平面
平面![]() ,进而可证得
,进而可证得![]() ;
;
(2)证明出![]() 平面
平面![]() ,然后以点
,然后以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系,设
轴建立空间直角坐标系,设![]() ,利用直线
,利用直线![]() 与平面所成的角为
与平面所成的角为![]() 求出
求出![]() ,然后利用空间向量法可求得二面角
,然后利用空间向量法可求得二面角![]() 的平面角的大小.
的平面角的大小.
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,
,

![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() .
.
![]() 四边形
四边形![]() 是菱形,且
是菱形,且![]() ,
,![]() 是正三角形,则
是正三角形,则![]() .
.
又![]() ,
,![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,![]() ;
;
(2)![]() ,平面
,平面![]() 平面
平面![]() ,交线为
,交线为![]() ,
,![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,![]() ,
,![]() 、
、![]() 、
、![]() 两两互相垂直.
两两互相垂直.
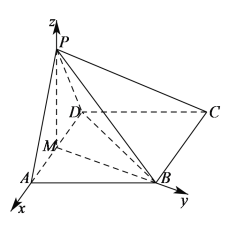
![]() 以
以![]() 为原点,
为原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
![]() 面
面![]() ,
,![]() 即为
即为![]() 与面
与面![]() 所成角,
所成角,![]() ,
,![]() .
.
在正三角形![]() 中,
中,![]() ,假设
,假设![]() ,则
,则![]() .
.
![]() 、
、![]() 、
、![]() 、
、![]() .
.
![]() ,
,![]() ,
,![]() .
.
设面![]() 的法向量为
的法向量为![]() ,则
,则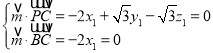 .
.
不妨取![]() ,则
,则![]() .
.
同理,设面![]() 的法向量为
的法向量为![]() ,则
,则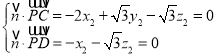 .
.
不妨取![]() ,则
,则![]() .
.
![]() ,
,![]() 平面
平面![]() 平面
平面![]() ,
,![]() 二面角
二面角![]() 平面角为
平面角为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某单位在2019年重阳节组织50名退休职工(男、女各25名)旅游,退休职工可以选择到甲、乙两个景点其中一个去旅游.他们最终选择的景点的结果如下表:
男性 | 女性 | |
甲景点 | 20 | 10 |
乙景点 | 5 | 15 |
(1)据此资料分析,是否有![]() 的把握认为选择哪个景点与性别有关?
的把握认为选择哪个景点与性别有关?
(2)按照游览不同景点用分层抽样的方法,在女职工中选取5人,再从这5人中随机抽取2人进行采访,求这2人游览的景点不同的概率.
附: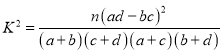 ,
,![]() .
.
P( | 0.010 | 0.005 | 0.001 |
k | 6.635 | 7.879 | 10.828 |