题目内容
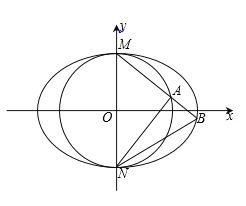
【题目】已知圆![]() 与椭圆
与椭圆![]() 相交于点M(0,1),N(0,-1),且椭圆的离心率为
相交于点M(0,1),N(0,-1),且椭圆的离心率为![]() .
.
(1)求![]() 的值和椭圆C的方程;
的值和椭圆C的方程;
(2)过点M的直线![]() 交圆O和椭圆C分别于A,B两点.
交圆O和椭圆C分别于A,B两点.
①若![]() ,求直线
,求直线![]() 的方程;
的方程;
②设直线NA的斜率为![]() ,直线NB的斜率为
,直线NB的斜率为![]() ,问:
,问:![]() 是否为定值? 如果是,求出定值;如果不是,说明理由.
是否为定值? 如果是,求出定值;如果不是,说明理由.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]()
【解析】
(1)由交点M(0,1)可求b,由离心率可求a,从而得到椭圆方程;(2)①设出直线l的方程,分别联立椭圆方程和圆的方程,解出A,B两点的坐标,由![]() 得到关于k的方程,求解即可得到结果;②结合①中A,B两点的坐标,利用斜率公式直接用k表示
得到关于k的方程,求解即可得到结果;②结合①中A,B两点的坐标,利用斜率公式直接用k表示![]() 和
和![]() ,由此可求得结果.
,由此可求得结果.
(1)因为圆![]() 与椭圆
与椭圆![]() 相交于点M(0,1)所以b=r=1.又离心率为
相交于点M(0,1)所以b=r=1.又离心率为![]() ,所以
,所以![]() ,所以椭圆
,所以椭圆![]() .
.
(2)①因为过点M的直线l另交圆O和椭圆C分别于A,B两点,所以设直线l的方程为![]() ,由
,由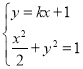 ,得
,得![]() ,
,
则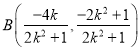 ,同理
,同理![]() ,解得
,解得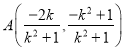 ,
,
因为![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() ,即直线l的方程为
,即直线l的方程为![]() .
.
②根据①,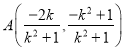 ,
,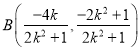 ,
,
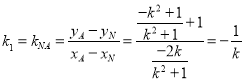 ,
,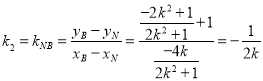 ,
,
所以![]() 为定值.
为定值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目