题目内容
【题目】已知M为圆C:x2+y2-4x-14y+45=0上任意一点,且点Q(-2,3).
(1)求|MQ|的最大值和最小值;
(2)若M(m,n),求![]() 的最大值和最小值
的最大值和最小值
【答案】(1)6![]() ,2
,2![]() (2)最大值为2+
(2)最大值为2+![]() ,最小值为2-
,最小值为2-![]()
【解析】
试题(1)求圆上的点到定点的距离最值,首先求圆心到直线的距离,再此基础上加减半径得到距离的最大值和最小值;(2)![]() 看作两点
看作两点![]() 连线的斜率,结合图形可知斜率的最值为直线与圆相切时的切线斜率
连线的斜率,结合图形可知斜率的最值为直线与圆相切时的切线斜率
试题解析:(1)由C:x2+y2-4x-14y+45=0可得(x-2)2+(y-7)2=8,
∴圆心C的坐标为(2,7),半径r=2![]() .
.
又|QC|=![]() =4
=4![]() .∴|MQ|max=4
.∴|MQ|max=4![]() +2
+2![]() =6
=6![]() ,
,
|MQ|min=4![]() -2
-2![]() =2
=2![]() .
.
(2)可知![]() 表示直线MQ的斜率,设直线MQ的方程为y-3=k(x+2),
表示直线MQ的斜率,设直线MQ的方程为y-3=k(x+2),
即kx-y+2k+3=0,则![]() =k.由直线MQ与圆C有交点,
=k.由直线MQ与圆C有交点,
所以![]() ≤2
≤2![]() .可得2-
.可得2-![]() ≤k≤2+
≤k≤2+![]() ,
,
所以![]() 的最大值为2+
的最大值为2+![]() ,最小值为2-
,最小值为2-![]() .
.

【题目】某手机公司生产某款手机,如果年返修率不超过千分之一,则生产部门当年考核优秀,现获得该公司2010-2018年的相关数据如下表所示:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年生产量(万台) | 3 | 4 | 5 | 6 | 7 | 7 | 9 | 10 | 12 |
产品年利润(千万元) | 3.6 | 4.1 | 4.4 | 5.2 | 6.2 | 7.8 | 7.5 | 7.9 | 9.1 |
年返修量(台) | 47 | 42 | 48 | 50 | 92 | 83 | 72 | 87 | 90 |
(1)从该公司2010-2018年的相关数据中任意选取3年的数据,以![]() 表示3年中生产部门获得考核优秀的次数,求
表示3年中生产部门获得考核优秀的次数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)根据散点图发现2015年数据偏差较大,如果去掉该年的数据,试用剩下的数据求出年利润![]() (千万元)关于年生产量
(千万元)关于年生产量![]() (万台)的线性回归方程(精确到0.01).部分计算结果:
(万台)的线性回归方程(精确到0.01).部分计算结果:![]() ,
,![]() ,
,![]() .
.
附: ;线性回归方程
;线性回归方程![]() 中,
中, ,
,![]() .
.
【题目】随着人民生活水平的日益提高,某小区居民拥有私家车的数量与日俱增.由于该小区建成时间较早,没有配套建造地下停车场,小区内无序停放的车辆造成了交通的拥堵.该小区的物业公司统计了近五年小区登记在册的私家车数量(累计值,如124表示2016年小区登记在册的所有车辆数,其余意义相同),得到如下数据:
编号 | 1 | 2 | 3 | 4 | 5 |
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
数量 | 34 | 95 | 124 | 181 | 216 |
(1)若私家车的数量![]() 与年份编号
与年份编号![]() 满足线性相关关系,求
满足线性相关关系,求![]() 关于
关于![]() 的线性回归方程,并预测2020年该小区的私家车数量;
的线性回归方程,并预测2020年该小区的私家车数量;
(2)小区于2018年底完成了基础设施改造,划设了120个停车位,为解决小区车辆乱停乱放的问题,加强小区管理,物业公司决定禁止无车位的车辆进入小区,由于车位有限,物业公司决定在2019年度采用网络竞拍的方式将车位对业主出租,租期一年,竞拍方案如下:
①截至2018年已登记在册的私家车业主拥有竞拍资格;
②每车至多申请一个车位,由车主在竞拍网站上提出申请并给出自己的报价;
③根据物价部门的规定,竞价不得超过1200元;
④申请阶段截止后,将所有申请的业主报价自高到低排列,排在前120位的业主以其报价成交;
⑤若最后出现并列的报价,则以提出申请的时间在前的业主成交,为预测本:次竞拍的成交最低价,物业公司随机抽取了有竞拍资格的40位业主进行竞拍意向的调查,统计了他们的拟报竞价,得到如下频率分布直方图:
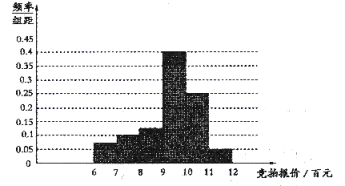
(ⅰ)求所抽取的业主中有意向竞拍报价不低于1000元的人数;
(ⅱ)如果所有符合条件的车主均参与竞拍,利用样木估计总体的思想,请你据此预测至少需要报价多少元才能竞拍车位成功?(精确到整数)
参考公式:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: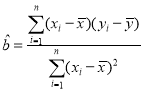
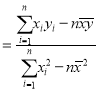 ,
,![]()
【题目】为预防![]() 病毒爆发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于
病毒爆发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于![]() %,则认为测试没有通过),公司选定
%,则认为测试没有通过),公司选定![]() 个流感样本分成三组,测试结果如下表:
个流感样本分成三组,测试结果如下表:
|
|
| |
疫苗有效 |
|
|
|
疫苗无效 |
|
|
|
已知在全体样本中随机抽取![]() 个,抽到
个,抽到![]() 组疫苗有效的概率是
组疫苗有效的概率是![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)现用分层抽样的方法在全体样本中抽取![]() 个测试结果,问应在
个测试结果,问应在![]() 组抽取多少个?
组抽取多少个?
(Ⅲ)已知![]() ,
,![]() ,求不能通过测试的概率.
,求不能通过测试的概率.