题目内容
已知函数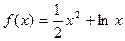 (1)求函数
(1)求函数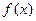 在区间[1,
在区间[1,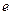 ]上的最大值、最小值;
]上的最大值、最小值;
(2)求证:在区间(1,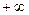 )上,函数
)上,函数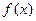 图象在函数
图象在函数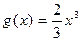 图象的下方;
图象的下方;
(3)设函数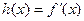 ,求证:
,求证: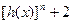 ≥
≥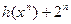 。(
。(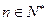 )
)
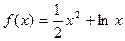 (1)求函数
(1)求函数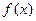 在区间[1,
在区间[1,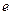 ]上的最大值、最小值;
]上的最大值、最小值;(2)求证:在区间(1,
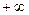 )上,函数
)上,函数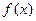 图象在函数
图象在函数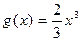 图象的下方;
图象的下方;(3)设函数
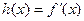 ,求证:
,求证: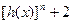 ≥
≥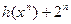 。(
。(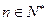 )
)(Ⅰ) 当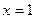 时,
时,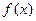 有最小值
有最小值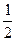 ;当
;当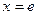 时,
时,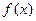 有最大值
有最大值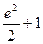 (Ⅱ) 见解析 (Ⅲ)见解析
(Ⅱ) 见解析 (Ⅲ)见解析
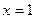 时,
时,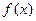 有最小值
有最小值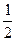 ;当
;当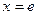 时,
时,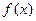 有最大值
有最大值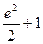 (Ⅱ) 见解析 (Ⅲ)见解析
(Ⅱ) 见解析 (Ⅲ)见解析(1) =
=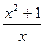 ,令
,令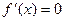 ,得
,得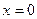
当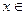 [1,
[1,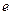 ]时,
]时,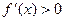 ,则
,则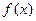 在区间[1,
在区间[1,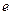 ]上是增函数
]上是增函数
∴ 当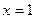 时,
时,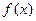 有最小值
有最小值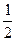 ;当
;当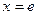 时,
时,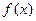 有最大值
有最大值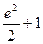 ………4分
………4分
(2)设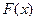 =
=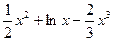 ,则
,则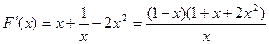
∵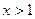 ,
, 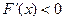 ∴
∴ 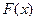 在区间(1,
在区间(1,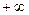 )上是减函数 又∵
)上是减函数 又∵ 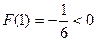
∴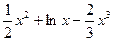
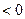 ,即
,即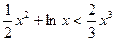 ,
,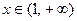
∴在区间(1,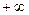 )上,函数
)上,函数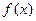 图象在函数
图象在函数 图象的下方
图象的下方
(3)当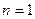 时,左边=
时,左边=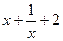 ,右边=
,右边=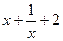 ,不等式成立;
,不等式成立;
当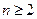 时,
时,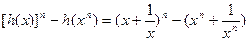
=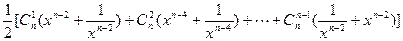
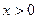 ∴
∴ 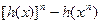 ≥
≥
∴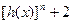 ≥
≥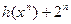 .
.
 =
=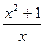 ,令
,令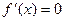 ,得
,得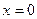
当
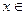 [1,
[1,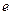 ]时,
]时,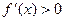 ,则
,则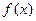 在区间[1,
在区间[1,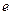 ]上是增函数
]上是增函数∴ 当
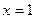 时,
时,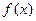 有最小值
有最小值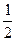 ;当
;当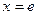 时,
时,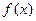 有最大值
有最大值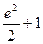 ………4分
………4分(2)设
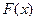 =
=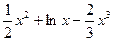 ,则
,则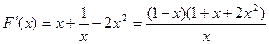
∵
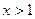 ,
, 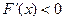 ∴
∴ 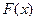 在区间(1,
在区间(1,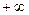 )上是减函数 又∵
)上是减函数 又∵ 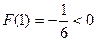
∴
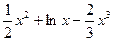
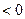 ,即
,即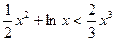 ,
,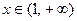
∴在区间(1,
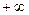 )上,函数
)上,函数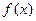 图象在函数
图象在函数 图象的下方
图象的下方 (3)当
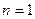 时,左边=
时,左边=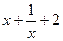 ,右边=
,右边=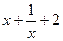 ,不等式成立;
,不等式成立;当
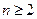 时,
时,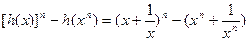
=
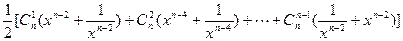
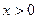 ∴
∴ 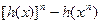 ≥
≥
∴
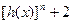 ≥
≥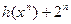 .
. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
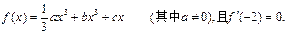
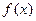 在x=2处取得极小值-2,求
在x=2处取得极小值-2,求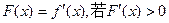 的解集是A,且A∪(0,1)=(-∞,1),求
的解集是A,且A∪(0,1)=(-∞,1),求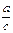 的最大值.
的最大值.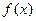 在开区间
在开区间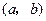 内可导,那么
内可导,那么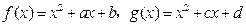 ,又
,又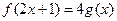 ,
,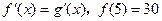 ,求
,求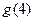 的值.
的值.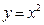 的图象,求出其在点
的图象,求出其在点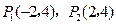 处的切线方程,并画出切线.
处的切线方程,并画出切线.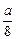 .
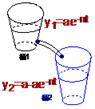
. 
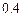 米的正方形
米的正方形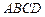 ,点E、F分别在边BC和CD上, △
,点E、F分别在边BC和CD上, △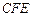 、△
、△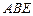 和四边形
和四边形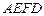 均由单一材料制成,制成△
均由单一材料制成,制成△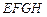 .
.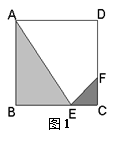
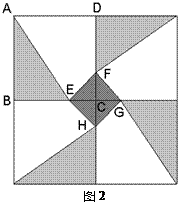
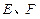 在什么位置时,定制这批地砖所需的材料费用最省?
在什么位置时,定制这批地砖所需的材料费用最省?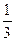
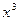 -2在点(-1,
-2在点(-1,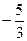 )处切线的倾斜角为( )
)处切线的倾斜角为( )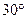 B
B 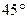 C
C 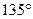 D
D 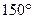
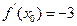 ,则
,则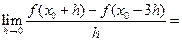 ( )
( )