题目内容
 (2011•潍坊二模)如图,已知定点F(-1,0),N(1,0),以线段FN为对角线作周长是4
(2011•潍坊二模)如图,已知定点F(-1,0),N(1,0),以线段FN为对角线作周长是4| 2 |
| GO |
(I)求点E、M所在曲线C1的方程及动点G的轨迹C2的方程;
(Ⅱ)已知过点F的直线l交曲线C1于点P、Q,交轨迹C2于点A、B,若|
| AB |
| 3 |
| 15 |
分析:(I)根据椭圆的定义,可得曲线C1是以F、N为焦点的椭圆,由题中数据即可求出曲线C1的方程为
+y2=1;再由圆的定义即可得到动点G的轨迹C2的方程为x2+y2=4;
(II)由题意得直线l与x轴不垂直,设l方程为y=k(x+1),利用点到直线的距离公式结合垂径定理,算出|AB|=2
.设P(x1,y1)、Q(x2,y2),△NPQ内切圆半径r满足
|NF|•|y1-y2|=
•r•(|PN|+|PQ|+|QN|),结合题中数据得到r=
|y1-y2|,由直线方程与椭圆消去x,得关于y的二次方程,再利用根与系数的关系算出|y1-y2|关于k的式子,从而得到r关于k的函数关系式,结合函数的单调性讨论可得r的取值范围.
| x2 |
| 2 |
(II)由题意得直线l与x轴不垂直,设l方程为y=k(x+1),利用点到直线的距离公式结合垂径定理,算出|AB|=2
3+
|
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
解答:解:(I)∵四边形MNEF是平行四边形,周长为4
∴点E到点F、N的距离之和等于2
(定长),且|NF|=2<2
由椭圆的定义,得曲线C1的方程为
+
=1(a>b>0)
可得a=
,c=1,b2=a2-c2=1,
∴曲线C1的方程为
+y2=1
∵|
|=2,∴动点G的轨迹为以原点为圆心,半径为2的圆
即曲线C2的方程为x2+y2=4;
(II)当l垂直x轴时,令x=-1代入曲线C2的方程得y=±
∴|AB|=2
∉(2
,
),不符合题意
因此直线l与x轴不垂直,设l方程为y=k(x+1)
原点到直线l的距离为d=
,
由圆的几何性质,得到|AB|=2
=2
=2
由|AB|∈(2
,
),解之得k2>
联解
,消去x得(2+
)y2-
y-1=0
设P(x1,y1),Q(x2,y2),△NPQ内切圆的半径为r
可得y1+y2=
=
,y1y2=-
=-
∵
|NF|•|y1-y2|=
•r•(|PN|+|PQ|+|QN|),其中|NF|=2,|PN|+|PQ|+|QN|=4
∴r=
|y1-y2|
而|y1-y2|=
=
=
∵k2>
,∴1-
>
另外,因为1-
<1,即
<|y1-y2|<
,可得r=
|y1-y2|∈(
,
)
∴△NPQ内切圆的半径的取值范围为(
,
).
| 2 |
∴点E到点F、N的距离之和等于2
| 2 |
| 2 |
由椭圆的定义,得曲线C1的方程为
| x2 |
| a2 |
| y2 |
| b2 |
可得a=
| 2 |
∴曲线C1的方程为
| x2 |
| 2 |
∵|
| GO |
即曲线C2的方程为x2+y2=4;
(II)当l垂直x轴时,令x=-1代入曲线C2的方程得y=±
| 3 |
∴|AB|=2
| 3 |
| 3 |
| 15 |
因此直线l与x轴不垂直,设l方程为y=k(x+1)
原点到直线l的距离为d=
| |k| | ||
|
由圆的几何性质,得到|AB|=2
| r2-d2 |
4-
|
3+
|
由|AB|∈(2
| 3 |
| 15 |
| 1 |
| 3 |
联解
|
| 1 |
| k2 |
| 2 |
| k |
设P(x1,y1),Q(x2,y2),△NPQ内切圆的半径为r
可得y1+y2=
| ||
2+
|
| 2k |
| 2k2+1 |
| 1 | ||
2+
|
| 2k2 |
| 2k2+1 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
∴r=
| ||
| 4 |
而|y1-y2|=
| (y1+y2)2-4y 1y2 |
(
|
2[1-
|
∵k2>
| 1 |
| 3 |
| 1 |
| (2k2+1)2 |
| 16 |
| 25 |
另外,因为1-
| 1 |
| (2k2+1)2 |
| 4 |
| 5 |
| 2 |
| 2 |
| ||
| 4 |
| 2 |
| 5 |
| 1 |
| 2 |
∴△NPQ内切圆的半径的取值范围为(
| 2 |
| 5 |
| 1 |
| 2 |
点评:本题给出动点轨迹,求轨迹的方程并讨论截得三角形内切圆半径的取值范围.着重考查了点到直线的距离公式、垂直定理、一元二次方程根与系数的关系和函数单调性等知识,属于难题.

练习册系列答案
相关题目
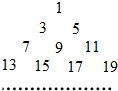 (2011•潍坊二模)已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是
(2011•潍坊二模)已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是 (2011•潍坊二模)运行如图的程序框图,当输入m=-4时的输出结果为n,若变量x,y满足
(2011•潍坊二模)运行如图的程序框图,当输入m=-4时的输出结果为n,若变量x,y满足