Question

设是非零实数，则方程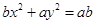及所表示的图形可能是（  ）

Answer 1

C

解析试题分析：对于A中，由于直线斜率为负数，说明了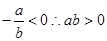，那么只能是为正数，可知知道的第一个方程表示的为椭圆，因此错误。
对于B，直线的方程不过原点，排除B。
对于C，由于直线斜率为正，那么可知，那么可知方程一表示的为双曲线，焦点在x轴上，成立。
对于D，由于由于直线斜率为正，那么可知，那么方程一不会是椭圆，故排除，故选C.
考点：本试题考查函数图像。
点评：解决该试题的关键是从直线入手确定参数的符号，进而确定图像直线的单调性，以焦点的位置，属于基础题。