题目内容
已知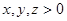 ,则
,则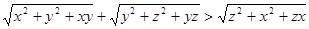
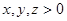 ,则
,则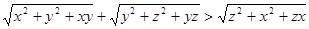
利用三角形的三边的不等关系,通过构造共顶点的三个120度的角,来分析证明得到。
本试题考查了不等式的证明
试题分析:证如下:
作ÐAOB = ÐBOC = ÐCOA = 120°,
设|OA| = x, |OB| = y, |OC| = z
两边之和小于第三边得证。
(不等式证明方法很多,请阅卷老师酌情给分)
点评:对于不等式的证明,可以构造函数来结合函数的单调性来得到不等式的关系,也可以直接运用均值不等式来放缩得到结论,也可以结合两点的距离公式理解不等式来求解得到,是一道有难度的试题。
试题分析:证如下:
作ÐAOB = ÐBOC = ÐCOA = 120°,
设|OA| = x, |OB| = y, |OC| = z
两边之和小于第三边得证。
(不等式证明方法很多,请阅卷老师酌情给分)
点评:对于不等式的证明,可以构造函数来结合函数的单调性来得到不等式的关系,也可以直接运用均值不等式来放缩得到结论,也可以结合两点的距离公式理解不等式来求解得到,是一道有难度的试题。

练习册系列答案
相关题目
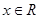 ,
, 恒成立(其中
恒成立(其中 ),求
),求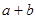 的最大值.
的最大值.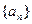 中,
中,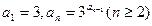 ,求
,求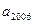 的末位数字是 。
的末位数字是 。 ,
,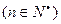


 ,且
,且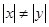 ,求
,求 的最小值.
的最小值.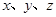 满足
满足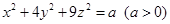 ,且
,且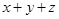 的最大值是7,求
的最大值是7,求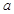 的值.
的值.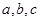 均为正实数,且
均为正实数,且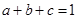 .求
.求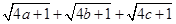 的最大值.
的最大值.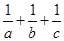 的最小值为( )
的最小值为( )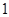 ,则圆锥的体积为 .
,则圆锥的体积为 .