题目内容
8.函数$f(x)=\frac{{\sqrt{4-x}}}{x-1}$的定义域为( )| A. | [-∞,4] | B. | [4,+∞) | C. | (-∞,4) | D. | (-∞,1)∪(1,4] |
分析 根据二次个数的性质以及分母不为0,得到关于x的不等式组,解出即可.
解答 解:由题意得:$\left\{\begin{array}{l}{4-x≥0}\\{x-1≠0}\end{array}\right.$,
解得:x≤4且x≠1,
故函数的定义域为:{x|x≤4且x≠1},
故选:D.
点评 本题考查了求函数的定义域问题,是一道基础题.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
18.若x∈(0,$\frac{π}{2}$),sinxcosx=$\frac{1}{2}$,则$\frac{1}{1+sinx}$+$\frac{1}{1+cosx}$=4-2$\sqrt{2}$.
17.已知函数y=f(x)在区间(0,3)上为增函数,y=g(x)在区间(2,5)上为减函数,则函数y=f(g(x))在区间(2,3)上为( )
| A. | 增函数 | B. | 减函数 | C. | 先增后减 | D. | 单调性不能确定 |
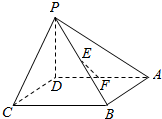 如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,且PD=AB=2a,E是PB的中点,F是AD的中点,求证:EF⊥平面PCB.
如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,且PD=AB=2a,E是PB的中点,F是AD的中点,求证:EF⊥平面PCB.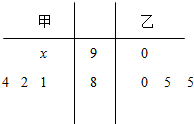 如图用茎叶图记录了同班的甲、乙两名学生4次数学考试成绩,其中甲的一次成绩模糊不清,用x标记.
如图用茎叶图记录了同班的甲、乙两名学生4次数学考试成绩,其中甲的一次成绩模糊不清,用x标记.