题目内容
已知在直三棱柱ABC-A1B1C1中,AB=4,AC=BC=3,D为AB的中点.
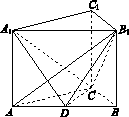
(Ⅰ)求异面直线CC1和AB的距离;
(Ⅱ)若AB1⊥A1C,求二面角A1-CD-B1的平面角的余弦值.

(Ⅰ)求异面直线CC1和AB的距离;
(Ⅱ)若AB1⊥A1C,求二面角A1-CD-B1的平面角的余弦值.
(Ⅰ)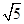 ; (Ⅱ)
; (Ⅱ)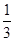 .
.
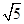 ; (Ⅱ)
; (Ⅱ)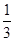 .
.试题分析:(Ⅰ) 在直三棱柱ABC-A1B1C1中, AC=BC=3,D为AB的中点,易知CD⊥AB.又侧棱垂直底面,从而有CC1⊥CD,即CD为异面直线CC1和AB的距离,计算其长度即可;(Ⅱ)易证CD垂直于侧面,从而CD⊥DA1,CD⊥DB1,故∠A1DB1为所求的二面角A1-CD-B1的平面角.再根据相关条件求出△A1DB1各边,从而利用余弦定理求出所求角的余弦值即可.
试题解析:(Ⅰ)因AC=BC,D为AB的中点,故CD⊥AB.
又直三棱柱中,CC1⊥面ABC,故CC1⊥CD,所以异面直线CC1和AB的距离为CD=
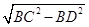 =
=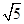 .
.5分
(Ⅱ)由CD⊥AB,CD⊥BB1,故CD⊥面A1ABB1,从而CD⊥DA1,CD⊥DB1,故∠A1DB1为所求的二面角A1-CD-B1的平面角. 8分
又CD⊥
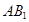 ,AB1⊥A1C,所以AB1⊥平面
,AB1⊥A1C,所以AB1⊥平面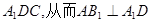 ,从而
,从而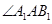 ,
,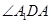 都与
都与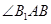 互余,因此
互余,因此 ,所以
,所以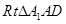 ∽
∽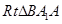 ,因此
,因此 =
=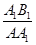 ,得
,得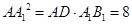 .从而A1D=
.从而A1D=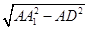 =2
=2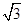 ,B1D=A1D=2
,B1D=A1D=2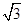 ,
,所以在△A1DB1中,由余弦定理得
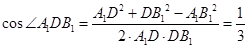 . 12分
. 12分
练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
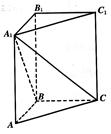
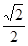 ,求点A到平面A1BC的距离.
,求点A到平面A1BC的距离. 的侧棱
的侧棱 两两垂直,且
两两垂直,且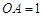 ,
,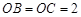 ,
,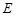 是
是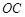 的中点。
的中点。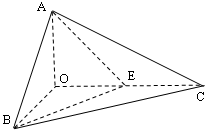
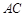 与
与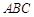 的所成角的正弦值。
的所成角的正弦值。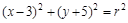 上有且只有两个点到直线
上有且只有两个点到直线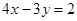 的距离为1,则半径
的距离为1,则半径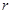 的取值范围( )
的取值范围( )
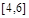
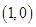 且与极轴垂直的直线交曲线
且与极轴垂直的直线交曲线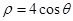 于
于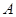 、
、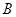 两点,则
两点,则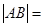 .
.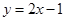 上,且A,B两点横坐标之差为
上,且A,B两点横坐标之差为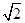 ,则A,B之间的距离为
,则A,B之间的距离为