题目内容
已知函数f(x)=alnx+bx,且f(1)=-1,f′(1)=0,
⑴求f(x);
⑵求f(x)的最大值;
⑶若x>0,y>0,证明:lnx+lny≤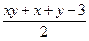 .
.
⑴求f(x);
⑵求f(x)的最大值;
⑶若x>0,y>0,证明:lnx+lny≤
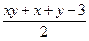 .
.(1)f(x)=lnx-x
(2)最大值为-1
(3)证明见解析。
本题主要考查函数、导数的基本知识、函数性质的处理以及不等式的综合问题,同时考查考生用函数放缩的方法证明不等式的能力.
⑴由b= f(1)=-1, f′(1)=a+b=0, ∴a=1,∴f(x)=lnx-x为所求;……………4分
⑵∵x>0,f′(x)=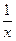 -1=
-1= ,
,
∴f(x)在x=1处取得极大值-1,即所求最大值为-1;……………8分
⑶由⑵得lnx≤x-1恒成立,
∴lnx+lny= +
+ ≤
≤ +
+ =
=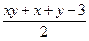 成立………12分
成立………12分
⑴由b= f(1)=-1, f′(1)=a+b=0, ∴a=1,∴f(x)=lnx-x为所求;……………4分
⑵∵x>0,f′(x)=
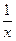 -1=
-1= ,
,| x | 0<x<1 | x=1 | x>1 |
| f′(x) | + | 0 | - |
| f(x) | ↗ | 极大值 | ↘ |
∴f(x)在x=1处取得极大值-1,即所求最大值为-1;……………8分
⑶由⑵得lnx≤x-1恒成立,
∴lnx+lny=
 +
+ ≤
≤ +
+ =
=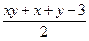 成立………12分
成立………12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
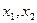 是函数
是函数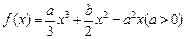 的两个极值点,且
的两个极值点,且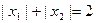
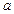 的取值范围;
的取值范围;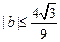 .
.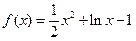 .
.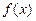 在区间
在区间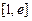 (
(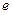 为自然对数的底)上的最大值和最小值;
为自然对数的底)上的最大值和最小值;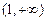 上,函数
上,函数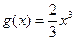 的图象的下方;
的图象的下方;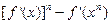 ≥
≥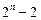
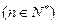 .
. (b、c为常数).
(b、c为常数).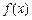 在
在
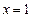 和
和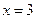 处取得极值,试求
处取得极值,试求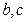 的值;
的值;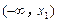 、
、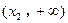 上单调递增,且在
上单调递增,且在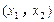 上单调递减,又满足
上单调递减,又满足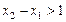 ,求证:
,求证: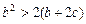 。
。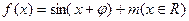 为奇函数,且过点
为奇函数,且过点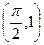 ,函数
,函数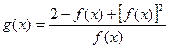 .
.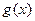 的解析式并求其定义域;
的解析式并求其定义域;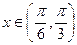 时不等式
时不等式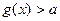 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.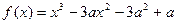
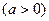
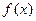 的单调区间;
的单调区间;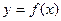 在点
在点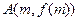 和
和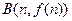
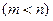 处的切线都与
处的切线都与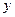 轴垂直,若曲线
轴垂直,若曲线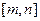 上与
上与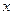 轴相交,求实数
轴相交,求实数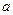 的取值范围;
的取值范围;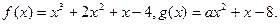
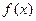 的极值;
的极值;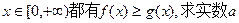 的取值范围。
的取值范围。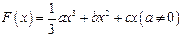 且
且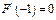
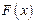 在
在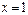 取得极小值-2,求函数
取得极小值-2,求函数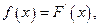 若
若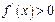 的解集为A,且
的解集为A,且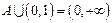 ,求
,求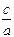 的范围
的范围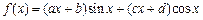 ,试确定常数
,试确定常数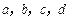 ,使得
,使得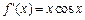 .
.