题目内容
【题目】已知函数![]() 在
在![]() 处取得极值.
处取得极值.
(1)讨论![]() 和
和![]() 是函数
是函数![]() 的极大值还是极小值;
的极大值还是极小值;
(2)过点![]() 作曲线
作曲线![]() 的切线,求此切线方程.
的切线,求此切线方程.
【答案】(1)见解析;(2)![]()
【解析】第一问由函数![]() 在
在![]() 处取得极值.
处取得极值.
说明了′(1)= ′(-1)=0,得到a,b的值,并代入原式中,判定函数的单调性,得到极值问题。
第二问中,要求过点![]() 作曲线
作曲线![]() 的切线,先设出切点坐标,然后结合导数的几何意义得到斜率,表示切线方程,再将A点代入方程中得到点的坐标,求解得到。
的切线,先设出切点坐标,然后结合导数的几何意义得到斜率,表示切线方程,再将A点代入方程中得到点的坐标,求解得到。
解:(1)′(x)=3ax2+2bx-3,依题意,′(1)= ′(-1)=0,即
3a+2b-3=0,
3a-2b-3=0.解得a=1, b="0."
∴(x)=x3-3x,′(x)=3x2-3=3(x+1)(x-1).
令′(x)=0,得x1=-1,x2=1.
若x∈(-∞,-1)∪(1,+∞),则′(x)>0,故(x)在(-∞,-1),(1,+∞)上是增函数.
若x∈(-1,1),则′(x)<0,故(x)在(-1,1)上是减函数.
所以(-1)=2是极大值,(1)=-2是极小值.
(1)曲线方程为y=x3-3x,点A(0,16)不在曲线上,设切点为M(x0,y0)
则点M的坐标满足y0= x03-3x0,
因为f’(x0)=3(x02-1),故切线方程为
y-y0=3(x02-1)(x-x9)
因为点A在曲线上,则可知16-(x03-3x0)=3(x02-1)(x-x9)
化简得到x0=-2,
所以切点坐标为M(-2,-2),切线方程为9x-y+16=0

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案【题目】为了更好地规划进货的数量,保证蔬菜的新鲜程度,某蔬菜商店从某一年的销售数据中,随机抽取了8组数据作为研究对象,如下图所示(![]() (吨)为买进蔬菜的质量,
(吨)为买进蔬菜的质量, ![]() (天)为销售天数):
(天)为销售天数):
| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(Ⅰ)根据上表数据在下列网格中绘制散点图;

(Ⅱ)根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅲ)根据(Ⅱ)中的计算结果,若该蔬菜商店准备一次性买进25吨,则预计需要销售多少天.
参考公式: 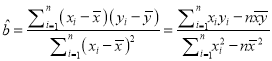 ,
, ![]() .
.
【题目】【2015高考陕西文数】随机抽取一个年份,对西安市该年4月份的天气情况进行统计,结果如下:
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
天气 | 晴 | 雨 | 阴 | 阴 | 阴 | 雨 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 晴 |
日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
天气 | 晴 | 阴 | 雨 | 阴 | 阴 | 晴 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 雨 |
(I)在4月份任取一天,估计西安市在该天不下雨的概率;
(II)西安市某学校拟从4月份的一个晴天开始举行连续两天的运动会,估计运动会期间不下雨的概率.