Question

【题目】已知椭圆方程为，双曲线的两条渐近线分别为， ，过椭圆的右焦点作直线，使，又与交于点，设直线与椭圆的两个交点由上至下依次为， ．　

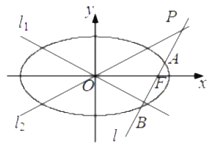
（1）若与所成的锐角为，且双曲线的焦距为4，求椭圆的方程；

（2）求的最大值．

Answer 1

【答案】（1）（2）最大值．

【解析】试题分析：（1）首先由题意并结合双曲线的性质可得出， 所满足的关系式，再与联立求出两者的值即可得出所求的椭圆的方程；（2）首先联立直线与的方程求出它们的交点的坐标，再令，利用引入的参数表示出点的坐标，由于点在椭圆上，代入椭圆的方程结合椭圆的性质求出的取值范围，即可得出所求的最大值．

试题解析： （1）双曲线的渐近线为，两渐近线夹角为60°，又，所以，

所以，所以．又，所以， ，所以椭圆的方程为，所以离心率．

（2）由已知， 与联立，解方程组得．设，则，因为，设，则，所以，即，将将A点坐标代入椭圆方程，得，

等式两边同除以， ，所以，当，即时， 有最大值，即的最大值为．