题目内容
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB.
(1)求证:CE⊥平面PAD;
(2)若PA=AB=1,AD=3,CD= ,∠CDA=45°,求四棱锥P-ABCD的体积.
,∠CDA=45°,求四棱锥P-ABCD的体积.

(1)求证:CE⊥平面PAD;
(2)若PA=AB=1,AD=3,CD=
 ,∠CDA=45°,求四棱锥P-ABCD的体积.
,∠CDA=45°,求四棱锥P-ABCD的体积.
(1) 见解析
(2)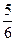
(2)
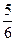
(1)证明:因为PA⊥平面ABCD,CE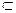 平面ABCD,所以PA⊥CE,
平面ABCD,所以PA⊥CE,
因为AB⊥AD,CE∥AB,所以CE⊥AD,又PA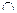 AD=A,所以CE⊥平面PAD
AD=A,所以CE⊥平面PAD
(2)解:由(1)可知CE⊥AD,在直角三角形ECD中,DE=CD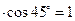 ,CE=CD
,CE=CD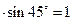 .
.
又因为AB=CE=1,AB∥CE,所以四边形ABCE为矩形,所以
 =
=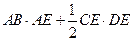 =
=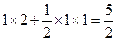 ,又PA⊥平面ABCD,PA=1,所以四棱锥P-ABCD的体积等于
,又PA⊥平面ABCD,PA=1,所以四棱锥P-ABCD的体积等于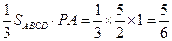
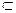 平面ABCD,所以PA⊥CE,
平面ABCD,所以PA⊥CE,因为AB⊥AD,CE∥AB,所以CE⊥AD,又PA
 AD=A,所以CE⊥平面PAD
AD=A,所以CE⊥平面PAD(2)解:由(1)可知CE⊥AD,在直角三角形ECD中,DE=CD
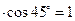 ,CE=CD
,CE=CD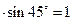 .
.又因为AB=CE=1,AB∥CE,所以四边形ABCE为矩形,所以
 =
=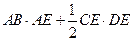 =
=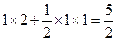 ,又PA⊥平面ABCD,PA=1,所以四棱锥P-ABCD的体积等于
,又PA⊥平面ABCD,PA=1,所以四棱锥P-ABCD的体积等于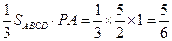

练习册系列答案
相关题目
 中,
中, ,
, ,
, °,平面
°,平面 平面
平面 ,
, ,
, 分别为
分别为 ,
, 中点.
中点. ∥平面
∥平面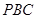 ;
;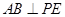 ;
; 的体积.
的体积.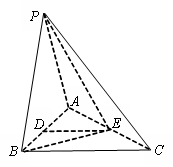

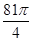
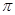


 的半圆面,则该圆锥的体积为 .
的半圆面,则该圆锥的体积为 . 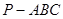 的各顶点都在一半径为
的各顶点都在一半径为 的球面上,球心
的球面上,球心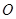 在
在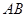 上,且有
上,且有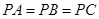 ,底面
,底面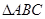 中
中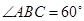 ,则球与三棱锥的体积之比是 .
,则球与三棱锥的体积之比是 . 的半圆面,则该圆锥的体积为________.
的半圆面,则该圆锥的体积为________.