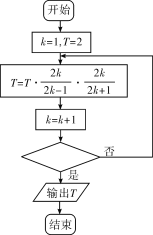
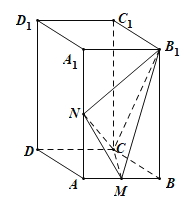
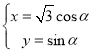题目内容
【题目】设椭圆E:![]() +
+![]() =1(a>b>0)的左、右焦点分别为F1,F2,过点F1的直线交椭圆E于A,B两点.若椭圆E的离心率为
=1(a>b>0)的左、右焦点分别为F1,F2,过点F1的直线交椭圆E于A,B两点.若椭圆E的离心率为![]() ,三角形ABF2的周长为4
,三角形ABF2的周长为4![]() .
.
(1)求椭圆E的方程;
(2)设不经过椭圆的中心而平行于弦AB的直线交椭圆E于点C,D,设弦AB,CD的中点分别为M,N,证明:O,M,N三点共线.
【答案】(1)![]() +
+![]() =1;(2)证明见解析
=1;(2)证明见解析
【解析】
(1)根据椭圆的定义由三角形ABF2的周长求出a,代入离心率求出c,再求出b,即可求得椭圆的方程;(2)直线斜率不存在时由椭圆的对称性即可证明;直线斜率存在时,设A(x1,y1),B(x2,y2),M(x0,y0),A,B 点的坐标代入方程,两式相减利用中点坐标公式变形可求出直线OM的斜率,同理可求出ON的斜率,两斜率相等即可得证.
(1)![]() ,
,![]() a=
a=![]() ,
,
又e=![]() ,∴c=
,∴c=![]() ,b=
,b=![]() ,
,
∴椭圆E的方程为![]() +
+![]() =1.
=1.
(2)当直线AB,CD的斜率不存在时,由椭圆的对称性知,中点M,N在x轴上,O,M,N三点共线;
当直线AB,CD的斜率存在时,设其斜率为k(k≠0),
且设A(x1,y1),B(x2,y2),M(x0,y0),
则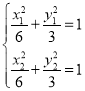 ,两式相减,得
,两式相减,得![]() =-
=-![]() ,
,
又![]() ,所以
,所以![]() ·
·![]() =-
=-![]() ,
,
则![]() -
-![]()
![]() -
-![]() .
.
同理可得![]() -
-![]() ,
,![]() ,∴O,M,N三点共线.
,∴O,M,N三点共线.

【题目】党的十九大明确把精准脱贫作为决胜全面建成小康社会必须打好的三大攻坚战之一.为坚决打赢脱贫攻坚战,某帮扶单位为帮助定点扶贫村脱贫,坚持扶贫同扶智相结合,此帮扶单位考察了甲、乙两种不同的农产品加工生产方式,现对两种生产方式的产品质量进行对比,其质量按测试指标可划分为:指标在区间![]() 的为优等品;指标在区间
的为优等品;指标在区间![]() 的为合格品,现分别从甲、乙两种不同加工方式生产的农产品中,各自随机抽取100件作为样本进行检测,测试指标结果的频数分布表如下:
的为合格品,现分别从甲、乙两种不同加工方式生产的农产品中,各自随机抽取100件作为样本进行检测,测试指标结果的频数分布表如下:
甲种生产方式:
指标区间 |
|
|
|
|
|
|
频数 | 5 | 15 | 20 | 30 | 15 | 15 |
乙种生产方式:
指标区间 |
|
|
|
|
|
|
频数 | 5 | 15 | 20 | 30 | 20 | 10 |
(1)在用甲种方式生产的产品中,按合格品与优等品用分层抽样方式,随机抽出5件产品,①求这5件产品中,优等品和合格品各多少件;②再从这5件产品中,随机抽出2件,求这2件中恰有1件是优等品的概率;
(2)所加工生产的农产品,若是优等品每件可售55元,若是合格品每件可售25元.甲种生产方式每生产一件产品的成本为15元,乙种生产方式每生产一件产品的成本为20元.用样本估计总体比较在甲、乙两种不同生产方式下,该扶贫单位要选择哪种生产方式来帮助该扶贫村来脱贫?