题目内容
【题目】已知函数![]() ,其中
,其中![]() 是自然对数的底数.
是自然对数的底数.
(1)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)如果对任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)讨论函数![]() 的零点个数.
的零点个数.
【答案】(1)![]() (2)
(2)![]() (3)当
(3)当![]() 时,函数
时,函数![]() 有一个零点;当
有一个零点;当![]() 时,
时,![]() 有三个零点.
有三个零点.
【解析】
(1)代入![]() 的函数解析式,求得导函数及切点坐标,由导数的几何意义即可得切线方程;
的函数解析式,求得导函数及切点坐标,由导数的几何意义即可得切线方程;
(2)求得导函数,并对![]() 分类讨论,即可确定
分类讨论,即可确定![]() 的单调性,进而由不等式恒成立求得
的单调性,进而由不等式恒成立求得![]() 的取值范围;
的取值范围;
(3)将![]() 的解析式代入可得
的解析式代入可得![]() 解析式,结合基本不等式可知在
解析式,结合基本不等式可知在![]() 时,函数
时,函数![]() 有唯一零点;当
有唯一零点;当![]() 时,可知
时,可知![]() 为奇函数,由
为奇函数,由![]() 可判断
可判断![]() 的单调情况,进而构造
的单调情况,进而构造![]() ,可证明当
,可证明当![]() 时,
时,![]() ,进而可知当
,进而可知当![]() 时,函数
时,函数![]() 有唯一零点,即可判断
有唯一零点,即可判断![]() 时
时![]() 的零点个数.
的零点个数.
(1)当![]() 时,
时,![]() ,
,
可得![]() ,
,
则有![]() ,
,![]() ,即切点坐标为
,即切点坐标为![]() ,
,
则切线方程为![]() ,
,
化简可得![]() .
.
(2)函数![]() ,
,
则![]() ,
,
当![]() 时,
时,![]() 恒成立,则函数
恒成立,则函数![]() 在
在![]() 上单增,而
上单增,而![]() ,与
,与![]() 恒成立矛盾,不合题意;
恒成立矛盾,不合题意;
当![]() 时,
时,![]() 恒成立,则符合题意;
恒成立,则符合题意;
当![]() 时,由
时,由![]() 得
得![]() ,则
,则![]() 在
在![]() 上单调递减,
上单调递减,
在![]() 上为单调递增,
上为单调递增,
则![]() ,解得
,解得![]() .
.
综上:![]() .
.
(3)因![]() ,
,
当![]() 时,因为
时,因为![]() 恒成立,
恒成立,
则![]() 在
在![]() 上为增函数,而
上为增函数,而![]() ,则此时函数
,则此时函数![]() 有唯一零点.
有唯一零点.
当![]() 时,
时,![]() 则
则![]() 为奇函数.
为奇函数.
只需研究![]() 情形.
情形.
由![]() ,
,
得![]() ,则有
,则有![]() .
.
则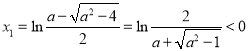 ,
,![]() ,
,
则![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,
上为增函数,
则有![]() .
.
下面证明:当![]() 时,
时,![]() .
.
证明:令![]() ,则
,则![]() ,
,![]() ,
,
即函数![]() 在
在![]() 上为增函数,故有
上为增函数,故有![]() ,
,
则![]() 在
在![]() 上为增函数,故有
上为增函数,故有![]() ,则
,则![]() .
.
当![]() 时,有
时,有![]() ,则
,则![]() ,
,
取![]() ,则
,则![]() ,
,
因为![]() 为连续函数,由零点存在性定理可得:存在唯一
为连续函数,由零点存在性定理可得:存在唯一![]() ,使得
,使得![]() ,即当
,即当![]() 时,函数
时,函数![]() 有唯一零点,也即此时函数
有唯一零点,也即此时函数![]() 有三个零点.
有三个零点.
综上:当![]() 时,函数
时,函数![]() 有一个零点;当
有一个零点;当![]() 时,
时,![]() 有三个零点.
有三个零点.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目