题目内容
17．
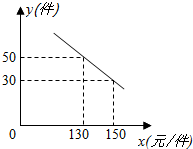某商场购进一种每件价格为100元的新商品，在商场试销发现：销售单价x（元/件）与每天销售量y（件）之间满足如图所示的关系：（1）求出y与x之间的函数关系式；
（2）写出每天的利润W与销售单价x之间的函数关系式；
若你是商场负责人，会将售价定为多少，来保证每天获得的利润最大，最大利润是多少？
分析 （1）设y与x之间的函数关系式为y=kx+b（k≠0），根据所给函数图象列出关于kb的关系式，求出k、b的值即可；
（2）把每天的利润W与销售单价x之间的函数关系式化为二次函数顶点式的形式，由此关系式即可得出结论．
解答 解：（1）设y与x之间的函数关系式为y=kx+b（k≠0），由所给函数图象得
$\left\{\begin{array}{l}{130k+b=50}\\{150k+b=30}\end{array}\right.$，解得k=-1，b=180
∴函数关系式为y=-x+180…（6分）
（2）W=（x-100）（-x+180）=-x2+280x-18000=-（x-140）2+1600
当售价定为140元，W最大=1600
∴售价定为140元/件时，每天最大利润W=1600元…（12分）
点评 本题考查的是二次函数的应用，根据题意列出关于k、b的关系式是解答此题的关键．
练习册系列答案
小学夺冠AB卷系列答案
相关题目
12．若loga$\frac{3}{5}$＜1，则a的取值范围是（ ）
| A． | 0＜a＜$\frac{3}{5}$ | B． | a＞$\frac{3}{5}$且a≠1 | C． | $\frac{3}{5}$＜a＜1 | D． | 0＜a＜$\frac{3}{5}$或a＞1 |
在△ABC中，内角A，B，C所对的边分别为a，b，c，已知$\frac{sinB}{sinA+sinC}$=$\frac{a+b-c}{a+b}$．