题目内容
7.已知f(x)=x3+f′($\frac{2}{3}$)x2-x,则f(x)的图象在点($\frac{2}{3}$,f($\frac{2}{3}$))处的切线斜率是-1.分析 根据f(x)解析式确定出f′(x)解析式,把x=$\frac{2}{3}$代入计算求出f′($\frac{2}{3}$)的值,即为所求切线的斜率.
解答 解:∵f(x)=x3+f′($\frac{2}{3}$)x2-x,
∴f′(x)=3x2+2f′($\frac{2}{3}$)x-1,
把x=$\frac{2}{3}$代入得:f′($\frac{2}{3}$)=3×($\frac{2}{3}$)2+2f′($\frac{2}{3}$)×$\frac{2}{3}$-1,
解得:f′($\frac{2}{3}$)=-1,
则f(x)的图象在点($\frac{2}{3}$,f($\frac{2}{3}$))处的切线斜率是-1,
故答案为:-1
点评 此题考查了利用导数研究曲线上某点切线方程,求出f(x)的导函数是解本题的关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
2.下列说法正确的是( )
| A. | 正数的n次方根是正数 | B. | 负数的n次方根是负数 | ||
| C. | 0的n次方根是0 | D. | $\root{n}{a}$是无理数 |
12.在等差数列{an}中,a1=1,a4=49,前n项和Sn=100,则公差d和项数n为( )
| A. | d=12,n=4 | B. | d=-18,n=2 | C. | d=16,n=3 | D. | d=16,n=4 |
19.已知Sn是等差数列{an}的前n项和,若a7=9a3,则$\frac{{S}_{9}}{{S}_{5}}$=( )
| A. | 9 | B. | 5 | C. | $\frac{18}{5}$ | D. | $\frac{9}{25}$ |
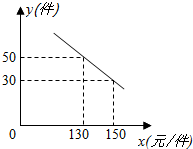 某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系:
某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系: