题目内容
2.已知抛物线y=ax2,直线l1,l2都过点(1,-2)且互相垂直,若抛物线与直线l1,l2中的至少一条有公共点,则a的取值范围是(0,$\frac{1}{8}$]..分析 先考虑抛物线与直线l1,l2没有公共点,由题意直线l1,l2的斜率分别设为k1,k2,过点P(1,-2)的直线设为y=k(x-1)-2,由由y=k(x-1)-2与抛物线y=ax2联立,得ax2-kx+k+2=0,由直线l1、l2都过点P(1,-2)且都与抛物线相切,知a≠0,△=k2-4ak-8a≥0,再由l1⊥l2,能求出a的取值范围,利用补集思想可得结论.
解答 解:先考虑抛物线与直线l1,l2没有公共点.
易知l1斜率存在,且不为0.设l1的斜率为k,则l1的斜率为-$\frac{1}{k}$,
则l1的方程为y+2=k(x-1),l2的方程为y+2=-$\frac{1}{k}$(x-1).
由$\left\{\begin{array}{l}{y=a{x}^{2}}\\{y+2=k(x-1)}\end{array}\right.$得,ax2-kx+k+2=0.
由l1与二次函数y=ax2(a>0)的图象没有公共点知,${△}_{1}={k}^{2}-4a(k+2)<0$…①.
同理,由l2与二次函数y=ax2(a>0)的图象没有公共点知,${△}_{2}=(-\frac{1}{k})^{2}-4a(-\frac{1}{k}+2)<0$…②.
由①得$2a-2\sqrt{{a}^{2}+2a}$<k<2a+2$\sqrt{{a}^{2}+2a}$;
由②得k<$\frac{a-\sqrt{{a}^{2}+2a}}{4a}$,或k>$\frac{a+\sqrt{{a}^{2}+2a}}{4a}$.
依题意,若方程组①②无解
∴$2a-2\sqrt{{a}^{2}+2a}$≥$\frac{a-\sqrt{{a}^{2}+2a}}{4a}$且2a+2$\sqrt{{a}^{2}+2a}$≤$\frac{a+\sqrt{{a}^{2}+2a}}{4a}$,即0<a≤$\frac{1}{8}$.
∴方程组①②有解?a>$\frac{1}{8}$.
∴抛物线与直线l1,l2中的至少一条有公共点,则a的取值范围是(0,$\frac{1}{8}$].
故答案为:(0,$\frac{1}{8}$].
点评 本题考查直线与抛物线的位置关系,考查正难则反的数学思想,考查学生分析解决问题的能力,有难度.

| A. | 4 | B. | -4 | C. | -5 | D. | ±4 |
| A. | 4i | B. | -4i | C. | 4 | D. | -4 |
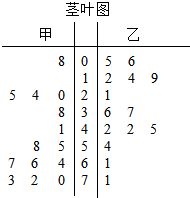 为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00-10:00间各自的点击量,得到如图茎叶图,则甲、乙两个网站点击量的中位数分别是( )
为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00-10:00间各自的点击量,得到如图茎叶图,则甲、乙两个网站点击量的中位数分别是( )| A. | 55,36 | B. | 55.5,36.5 | C. | 56.5,36.5 | D. | 58,37 |
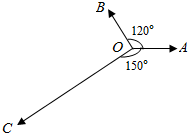 如图所示,平面内有三个向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$,$\overrightarrow{OA}$与$\overrightarrow{OB}$夹角为120°,$\overrightarrow{OA}$与$\overrightarrow{OC}$夹角为150°,且$|{\overrightarrow{OA}}|=|{\overrightarrow{OB}}|=1$,$|{\overrightarrow{OC}}|=2\sqrt{3}$,若$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}$(λ,μ∈R),则λ+μ=( )
如图所示,平面内有三个向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$,$\overrightarrow{OA}$与$\overrightarrow{OB}$夹角为120°,$\overrightarrow{OA}$与$\overrightarrow{OC}$夹角为150°,且$|{\overrightarrow{OA}}|=|{\overrightarrow{OB}}|=1$,$|{\overrightarrow{OC}}|=2\sqrt{3}$,若$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}$(λ,μ∈R),则λ+μ=( )