题目内容
【题目】已知数列
， 
满足
， 
，且
， 
.
（1）求
及
；
（2）猜想
， 
的通项公式，并证明你的结论；
（3）证明：对所有的
， 
.
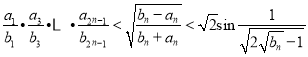【答案】（1）
， 
， 
， 
， 
， 
；（2）见解析；（3）见解析.
【解析】试题分析：（1）依次把n=1，2，3代入递推式即可求出{an}，{bn}的前4项；
（2）利用数学归纳法证明猜想；
（3）利用放缩法证明不等式左边，利用函数单调性证明不等式右边．
试题解析：
（1）因为
， 
，且
，
令
，得到
解得
， 
；同理令
分别解得由此可得
， 
，
， 
；
（2）证明：猜测
， 
，
用数学归纳法证明：①当
时，由上可得结论成立.
②假设当
时，结论成立，即
， 
，
那么当
时， 
，
，所以当
时，结论也成立.
由①②，可知
， 
对一切正整数都成立.
（3）由（2）知， 
，
于是所证明的不等式即为
（ⅰ）先证明： 
因为
，所以
，从而
，
即
，所以
（ⅱ）再证明
设函数
， 
，则
， 
.
因为在区间
上
为增函数，
所以当
时， 
，
从而
在区间
上为单调递减函数，
因此
对于一切
都成立，因为当
时， 
，
所以
综上所述，对所有的
，均有
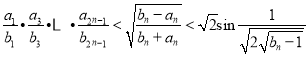成立.
练习册系列答案
相关题目
【题目】计划在某水库建一座至多安装
台发电机的水电站，过去
年的水文资料显示，水库年入流量
（年入流量：一年内上游来水与库区降水之和．单位：亿立方米）都在40以上，不足
的年份有
年，不低于
且不超过
的年份有
年，超过
的年份有
年，将年入流量在以上三段的频率作为相应段的概率，假设各年的年入流量相互独立．
（1）求未来
年中，设
表示流量超过
的年数，求
的分布列及期望；
（2）水电站希望安装的发电机尽可能运行，但每年发电机最多可运行台数受年入流量
限制，并有如下关系：
年入流量 |
|
|
|
发电机最多可运行台数 |
|
|
|
若某台发电机运行，则该台年利润为
万元，若某台发电机未运行，则该台年亏损
万元，欲使水电站年总利润的均值达到最大，应安装发电机多少台？
