题目内容
1.已知$\overrightarrow{a}$=(1,1),$\overrightarrow{b}$=(0,-2),当k为何值时:(1)k$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{a}$+$\overrightarrow{b}$共线;
(2)k$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{a}$+$\overrightarrow{b}$的夹角为120°;
(3)k$\overrightarrow{a}$-$\overrightarrow{b}$的模等于$\sqrt{10}$.
分析 (1)求得向量k$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{a}$+$\overrightarrow{b}$的坐标,由向量共线的坐标表示,解方程可得k;
(2)由向量的夹角公式,解方程即可得到k;
(3)运用向量的模的公式,计算即可得到所求k.
解答 解:(1)k$\overrightarrow{a}$-$\overrightarrow{b}$=(k,k+2),$\overrightarrow{a}$+$\overrightarrow{b}$=(1,-1),
由k$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{a}$+$\overrightarrow{b}$共线,可得-k=k+2,
解得k=-1,
即k=-1时,k$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{a}$+$\overrightarrow{b}$共线;
(2)k$\overrightarrow{a}$-$\overrightarrow{b}$=(k,k+2),$\overrightarrow{a}$+$\overrightarrow{b}$=(1,-1),
|k$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{2{k}^{2}+4k+4}$,|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{2}$,
由题意可得cos120°=$\frac{(k\overrightarrow{a}-\overrightarrow{b})•(\overrightarrow{a}+\overrightarrow{b})}{|k\overrightarrow{a}-\overrightarrow{b}|•|\overrightarrow{a}+\overrightarrow{b}|}$
=$\frac{-2}{\sqrt{2{k}^{2}+4k+4}•\sqrt{2}}$=-$\frac{1}{2}$,
解得k=-1±$\sqrt{7}$.
即k=-1±$\sqrt{7}$时,k$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{a}$+$\overrightarrow{b}$的夹角为120°;
(3)由题意可得|k$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{2{k}^{2}+4k+4}$=$\sqrt{10}$,
解得k=-3或1.
即k=-3或1时,k$\overrightarrow{a}$-$\overrightarrow{b}$的模等于$\sqrt{10}$.
点评 本题考查向量共线的坐标表示和向量的夹角公式,以及向量的模的公式的运用,考查运算能力,属于基础题.

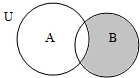
| A. | (CuA)∩B | B. | (CuB)∩A | C. | Cu(A∩B) | D. | Cu(A∪B) |
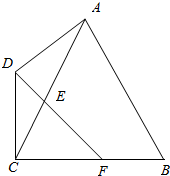 如图所示,平面四边形ABCD中,AB=AC=BC=$\sqrt{3}$,CD=AD=1,已知$\overrightarrow{AE}$=$λ\overrightarrow{AC}$,$\overrightarrow{CF}$=λ$\overrightarrow{CB}$,λ∈(0,1),且存在实数t使$\overrightarrow{CE}$=t$\overrightarrow{CD}$+(1-t)$\overrightarrow{CF}$,则$\overrightarrow{EA}$•$\overrightarrow{AB}$=( )
如图所示,平面四边形ABCD中,AB=AC=BC=$\sqrt{3}$,CD=AD=1,已知$\overrightarrow{AE}$=$λ\overrightarrow{AC}$,$\overrightarrow{CF}$=λ$\overrightarrow{CB}$,λ∈(0,1),且存在实数t使$\overrightarrow{CE}$=t$\overrightarrow{CD}$+(1-t)$\overrightarrow{CF}$,则$\overrightarrow{EA}$•$\overrightarrow{AB}$=( )| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | -$\frac{3}{4}$ | D. | -1 |