题目内容
已知f(x)是定义在R上的偶函数,对任意的x∈R都有f(x+4)=f(x)+f(2)成立.若f(0)=0,f(1)=2,则f(1) +f(2)+f(3)+…+f(2007)的值等于( )
|
A.2007 |
B.2008 |
C.2009 |
D.2010 |
【答案】
B
【解析】. (令x=-2即f(2)=f(-2)+f(2),∴f(-2)=0,又f(x)是偶函数,即f(2)=0,∴f(x+4)=f(x),故f(x)的周期为4.f(3)=f(-1)=f(1)=2,f(4)=f(0)=0.f(2008)=f(502×4)=f(0)=0.∴f(1)+f(2)+f(3)+…+f(2007)=f(1)+f(2)+f(3)+…+f (2007)+f (2008) =502[f(1)+f(2)+f(3)+f(4)]=2008,故选B.)

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 ) =
f(x)-f(y)
) =
f(x)-f(y) 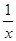 ) <2
) <2  ∪
∪ 上的奇函数,当
上的奇函数,当 时,f (x)的图象如图所示,那么f (x)的值域是
时,f (x)的图象如图所示,那么f (x)的值域是
