题目内容
11.已知空间几何体的正视图,侧视图都是边长为1,且一个内角为60°的菱形,而俯视图是个圆,则这一几何体的体积为$\frac{\sqrt{3}}{12}$π或$\frac{π}{4}$.分析 由三视图可得,几何体是由两个底面直径为1,母线长为1的圆锥组合而成,代入圆锥侧面积公式,即可求解.
解答  解:∵几何体的正视图、侧视图是周长为4一个内角为60°的菱形
解:∵几何体的正视图、侧视图是周长为4一个内角为60°的菱形
∴几何体是由两个底面直径为1,母线长为1的两个圆锥组合而成,或由两个底面直径为$\sqrt{3}$,母线长为1的两个圆锥组合而成,
∴V=2×$\frac{1}{3}$×($\frac{1}{2}$)2π×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{12}$π.
或V=2×$\frac{1}{3}$×($\frac{\sqrt{3}}{2}$)2π×$\frac{1}{2}$=$\frac{π}{4}$.
故答案为:$\frac{\sqrt{3}}{12}$π或$\frac{π}{4}$.
点评 本题考查的知识点是由三视图求面积,其中根据已知条件判断几何体的形状及底面直径和母线的长是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.设条件p:a>0,条件q:a2+a>0; 那么p就是q的( )
| A. | 充要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
16.在等比数列{an}中,如果a3=2,a6=6,那么a9为( )
| A. | 8 | B. | 10 | C. | 12 | D. | 18 |
20.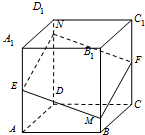 已知正方体ABCD-A1B1C1D1的棱长为1,E,F分别是边AA1,CC1的中点,点M是BB1上的动点,过点E,M,F的平面与棱DD1交于点N,设BM=x,平行四边形EMFN的面积为S,设y=S2,则y关于x的函数y=f(x)的解析式为( )
已知正方体ABCD-A1B1C1D1的棱长为1,E,F分别是边AA1,CC1的中点,点M是BB1上的动点,过点E,M,F的平面与棱DD1交于点N,设BM=x,平行四边形EMFN的面积为S,设y=S2,则y关于x的函数y=f(x)的解析式为( )
 已知正方体ABCD-A1B1C1D1的棱长为1,E,F分别是边AA1,CC1的中点,点M是BB1上的动点,过点E,M,F的平面与棱DD1交于点N,设BM=x,平行四边形EMFN的面积为S,设y=S2,则y关于x的函数y=f(x)的解析式为( )
已知正方体ABCD-A1B1C1D1的棱长为1,E,F分别是边AA1,CC1的中点,点M是BB1上的动点,过点E,M,F的平面与棱DD1交于点N,设BM=x,平行四边形EMFN的面积为S,设y=S2,则y关于x的函数y=f(x)的解析式为( )| A. | $f(x)=2{x^2}-2x+\frac{3}{2}$,x∈[0,1] | |
| B. | $f(x)=\left\{\begin{array}{l}\frac{3}{2}-x,x∈[0\;,\;\frac{1}{2})\\ x+\frac{1}{2},x∈[\frac{1}{2}\;,\;1].\end{array}\right.$ | |
| C. | $f(x)=\left\{\begin{array}{l}-2{x^2}+\frac{3}{2},x∈[0\;,\;\frac{1}{2}]\\-2{(x-1)^2}+\frac{3}{2},x∈(\frac{1}{2}\;,\;1].\end{array}\right.$ | |
| D. | $f(x)=-2{x^2}+2x+\frac{3}{2}$,x∈[0,1] |