题目内容
已知点P在圆C:x2+(y-3)2=1上,点Q在 =1的右支上,F是双曲线的左焦点,则|PQ|+|QF|的最小值( )
=1的右支上,F是双曲线的左焦点,则|PQ|+|QF|的最小值( )A.2
 +1
+1B.3+2

C.4+2

D.5+2

【答案】分析:先根据双曲线的定义把问题转化,再根据三角形三边所满足的关系即可求出结论.
解答: 解:如图,|PQ|+|QF|
解:如图,|PQ|+|QF|
=|CQ|-|CP|+|QF|
=|CQ|+|QF|-1
=|CQ|+|QF'|+2a-1
=|CQ|+|QF'|+2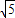 -1
-1
从图中可以看出,当F',Q,C三点共线时,|CQ|+|QF'|最小,其中F'( ,0)
,0)
则|PQ|+|QF|的最小值=|CF'|+2 -1=4+2
-1=4+2 -1=3+2
-1=3+2 .
.
故选B.
点评:本题主要考查了双曲线的简单性质.在解决涉及到圆锥曲线上的点与焦点之间的关系的问题中,圆锥曲线的定义往往是解题的突破口.
解答:
 解:如图,|PQ|+|QF|
解:如图,|PQ|+|QF|=|CQ|-|CP|+|QF|
=|CQ|+|QF|-1
=|CQ|+|QF'|+2a-1
=|CQ|+|QF'|+2
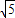 -1
-1从图中可以看出,当F',Q,C三点共线时,|CQ|+|QF'|最小,其中F'(
 ,0)
,0)则|PQ|+|QF|的最小值=|CF'|+2
 -1=4+2
-1=4+2 -1=3+2
-1=3+2 .
.故选B.
点评:本题主要考查了双曲线的简单性质.在解决涉及到圆锥曲线上的点与焦点之间的关系的问题中,圆锥曲线的定义往往是解题的突破口.

练习册系列答案
相关题目
 (2011•武昌区模拟)如图,已知点P是圆
(2011•武昌区模拟)如图,已知点P是圆