题目内容
已知线段PA⊥矩形ABCD所在平面,M、N分别是AB、PC的中点.
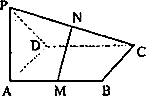
(Ⅰ)求证:MN//平面PAD;
(Ⅱ)当∠PDA=45°时,求证:MN⊥平面PCD
答案:
解析:
解析:
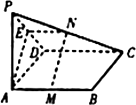
解:(Ⅰ)取PD的中点E,连接AE、EN

∵EN平行且等于![]() DC,而
DC,而![]() DC平行且等于AM
DC平行且等于AM
∴AMNE为平行四边形MN∥AE
∴MN∥平面PAD (6分)
(Ⅱ)∵PA⊥平面ABCD∴CD⊥PA又
∵ABCD为矩形 ∴CD⊥AD
∴CD⊥AE,AE∥MN,MN⊥CD (3分)
∵AD⊥DC,PD⊥DC ∴∠ADP=45°
又E是斜边的PD的中点∴AE⊥PD,
∴MN⊥PD∴MN⊥CD,∴MH⊥平面PCD (6分)

练习册系列答案
相关题目
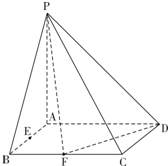 如图,已知四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD,AD=2,AB=1,E,F分别是线段AB.BC的中点.
如图,已知四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD,AD=2,AB=1,E,F分别是线段AB.BC的中点. (2012•即墨市模拟)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2a,AB=a,PA⊥平米ABCD,F是线段BC的中点.H为PD中点.
(2012•即墨市模拟)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2a,AB=a,PA⊥平米ABCD,F是线段BC的中点.H为PD中点. (2012•即墨市模拟)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2a,AB=a,PA⊥平米ABCD,F是线段BC的中点.H为PD中点.
(2012•即墨市模拟)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2a,AB=a,PA⊥平米ABCD,F是线段BC的中点.H为PD中点.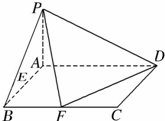 已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.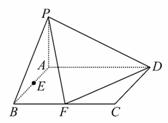 (3)若PB与平面ABCD所成的角为45°,求二面角A-PD-F的平面角的余弦值.
(3)若PB与平面ABCD所成的角为45°,求二面角A-PD-F的平面角的余弦值.