题目内容
【题目】某校高三有500名学生,在一次考试的英语成绩服从正态分布![]() ,数学成绩的频率分布直方图如下:
,数学成绩的频率分布直方图如下:
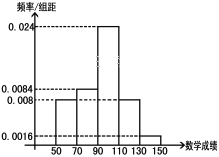
(Ⅰ)如果成绩大于135的为特别优秀,则本次考试英语、数学特别优秀的大约各多少人?
(Ⅱ)试问本次考试英语和数学的成绩哪个较高,并说明理由.
(Ⅲ)如果英语和数学两科都特别优秀的共有6人,从(Ⅰ)中的这些同学中随机抽取3人,设三人中两科都特别优秀的有![]() 人,求
人,求![]() 的分布列和数学期望。
的分布列和数学期望。
参考公式及数据:
若![]() ,则
,则![]() ,
,
![]() ,
,![]() .
.
【答案】(1)英语、数学特别优秀的大约各10,12; (2)英语的平均成绩更高; (3)![]()
【解析】
(1)先求出英语和数学特别优秀的的概率,由此能求出英语和数学都特别优秀的人数;
(2)分别计算得到英语和数学的平均分,比较平均分的大小,可得到结论;
(3)由题意得![]() 的所有可能的值为
的所有可能的值为![]() ,分别求出相应的概率,由此得到
,分别求出相应的概率,由此得到![]() 的分布列,求解数学期望.
的分布列,求解数学期望.
(1)![]() 英语成绩服从正态分布
英语成绩服从正态分布![]() ,
,
∴英语成绩特别优秀的概率为![]()
数学成绩特别优秀的概率为![]() ,
,
∴英语成绩特别优秀的同学有![]() 人,
人,
数学成绩特别优秀的同学有![]() 人.
人.
(2)英语的平均成绩为100分,数学的平均成绩为
![]()
因为![]() ,
,
所以英语的平均成绩更高.
(3)英语和数学都特别优秀的有6人,单科优秀的有10人,![]() 可取得值有0,1,2,3,
可取得值有0,1,2,3,
![]() ;
; ![]() ;
;
![]() ;
;![]()
故![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() 的数学期望为
的数学期望为![]() (人).
(人).
或:因![]() 服从超几何分布,所以
服从超几何分布,所以![]()

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目

