题目内容
17.已知共焦点的椭圆和双曲线的离心率分别为e1,e2,若椭圆的短轴长为双曲线虚轴长的2倍,则$\frac{1}{{e}_{1}}$+$\frac{1}{{e}_{2}}$的最大值为$\frac{5}{2}$.分析 设椭圆的短半轴是b1,双曲线的虚半轴是b2,半焦距都是c,由此求出椭圆与双曲线的离心率e1、e2;再求$\frac{1}{{e}_{1}}$+$\frac{1}{{e}_{2}}$的表达式,利用函数的导数求出它的最大值即可.
解答 解:设椭圆的短半轴是b1,双曲线的虚半轴是b2,它们的半焦距都是c;
则b1=2b2,
∴椭圆的长半轴是a1=$\sqrt{{{b}_{1}}^{2}{+c}^{2}}$=$\sqrt{{{4b}_{2}}^{2}{+c}^{2}}$,
双曲线的实半轴是a2=$\sqrt{{c}^{2}{{-b}_{2}}^{2}}$;
∴椭圆的离心率为e1=$\frac{c}{{a}_{1}}$,
双曲线的离心率为e2=$\frac{c}{{a}_{2}}$;
∴$\frac{1}{{e}_{1}}$+$\frac{1}{{e}_{2}}$=$\frac{{a}_{1}}{c}$+$\frac{{a}_{2}}{c}$
=$\frac{\sqrt{{{4b}_{2}}^{2}{+c}^{2}}}{c}$+$\frac{\sqrt{{c}^{2}{{-b}_{2}}^{2}}}{c}$
=$\sqrt{{4(\frac{{b}_{2}}{c})}^{2}+1}$+$\sqrt{{1-(\frac{{b}_{2}}{c})}^{2}}$;
∵0<b2<c,
∴0<$\frac{{b}_{2}}{c}$<1,
设$\frac{{b}_{2}}{c}$=x,x∈(0,1),
则函数y=$\sqrt{{4x}^{2}+1}$+$\sqrt{1{-x}^{2}}$,x∈(0,1);
求导数y′=$\frac{1}{2}$•$\frac{8x}{\sqrt{{4x}^{2}+1}}$+$\frac{1}{2}$•$\frac{-2x}{\sqrt{1{-x}^{2}}}$,
令y′=0,解得x=$\frac{\sqrt{3}}{2}$,
∴x=$\frac{\sqrt{3}}{2}$时,函数y取得最大值为ymax=2+$\frac{1}{2}$=$\frac{5}{2}$,
即$\frac{1}{{e}_{1}}$+$\frac{1}{{e}_{2}}$的最大值为$\frac{5}{2}$.
故答案为:$\frac{5}{2}$.
点评 本题考查了双曲线几何性质的应用问题,也考查了构造函数方法以及利用函数的导数求最值的问题,是综合性题目.

| A. | $\frac{3\sqrt{10}}{5}$ | B. | $\frac{18}{5}$ | C. | $\frac{16}{5}$ | D. | $\frac{12}{5}$ |
| A. | 0 | B. | $\frac{π}{4}$-$\frac{1}{2}$ | C. | $\frac{π}{4}$ | D. | 1-$\frac{π}{4}$ |
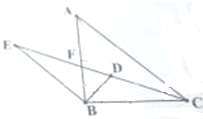 已知等腰直角三角形ABC中,∠ABC=90°,∠ABC和∠ACB的角平分线交于点D,延长CD交AC的平行线BE于点E.
已知等腰直角三角形ABC中,∠ABC=90°,∠ABC和∠ACB的角平分线交于点D,延长CD交AC的平行线BE于点E.