题目内容
【题目】如图,在棱长为a的正方体ABCD-A1B1C1D1中,M,N分别是AA1,D1C1的中点,过D,M,N三点的平面与正方体的下底面A1B1C1D1相交于直线l.

(1)画出直线l的位置,并简单指出作图依据;
(2)设l∩A1B1=P,求线段PB1的长.
【答案】(1)证明见解析;(2) ![]() .
.
【解析】
(1)根据点线面位置关系,三个平面两两相交,三条交线的可能情况分析,此题中的情况三条交线必交于一点,即可作图;
(2)利用平行关系结合三角形相似可求出PA1,再求出线段PB1的长.
(1)延长DM交D1A1的延长线于E,连接NE,则NE即为直线l的位置.
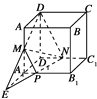
(2)∵M为AA1的中点,AD∥ED1,
∴AD=A1E=A1D1=![]() .
.
∵A1P∥D1N,且D1N=![]()
![]() ,
,
∴A1P=![]() D1N=
D1N=![]()
![]() ,
,
于是PB1=A1B1-A1P=![]() .
.

练习册系列答案
相关题目