题目内容
5.在锐角三角形ABC中,角A,B,C对边分别为a,b,c,B≠C,且a2sin(A+B)=(a2+c2-b2)sin(A+C).(1)求证:A=2B;
(2)求$\frac{b}{b+c}$的取值范围.
分析 (1)由已知及由余弦定理,正弦定理可得:sinAsinC=sinCsin2B,由C为锐角,sinC>0,解得:sinA=sin2B.结合A,B为锐角,即可得证.
(2)由A=2B,C=π-3B,A,B,C为锐角,可得$\frac{π}{6}$<B<$\frac{π}{4}$,解得1$<2co{s}^{2}B<\frac{3}{2}$,由正弦定理化简所求可得:$\frac{b}{b+c}$=$\frac{1}{2co{s}^{2}B}$∈($\frac{2}{3}$,1).
解答 解:(1)证明:∵a2sin(A+B)=(a2+c2-b2)sin(A+C).
∴a2sinC=(a2+c2-b2)sinB.
∴由余弦定理可得:a2sinC=2accosBsinB.即:asinC=csin2B.
∴由正弦定理可得:sinAsinC=sinCsin2B,
∵C为锐角,sinC>0,解得:sinA=sin2B.
∵A,B为锐角,
∴A=2B;
(2)∵A=2B∈(0,$\frac{π}{2}$),C=π-3B∈(0,$\frac{π}{2}$),
∴$\frac{π}{6}$<B<$\frac{π}{4}$,
∴$\frac{\sqrt{2}}{2}$<cosB<$\frac{\sqrt{3}}{2}$,解得:$\frac{1}{2}$<cos2B<$\frac{3}{4}$,可得:1$<2co{s}^{2}B<\frac{3}{2}$,
∴由正弦定理可得:$\frac{b}{b+c}$=$\frac{sinB}{sinB+sinC}$=$\frac{sinB}{sinB+sin(π-3B)}$=$\frac{sinB}{sinB+sin3B}$=$\frac{sinB}{2sin2BcosB}$=$\frac{1}{2co{s}^{2}B}$∈($\frac{2}{3}$,1).
点评 本题主要考查了正弦定理,余弦定理,三角函数的图象和性质的应用,属于基本知识的考查.

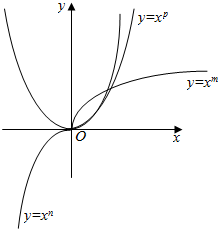
| A. | m>n>p | B. | m>p>n | C. | n>p>m | D. | p>n>m |