题目内容
【题目】已知两点
,若直线
上至少存在三个点
，使得
是直角三角形，则实数
的取值范围是（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】
当k=0时，M、N、P三点共线，构不成三角形，故k≠0．△MNP是直角三角形，由直径对的圆周角是直角，知直线和以MN为直径的圆有公共点即可，由此能求出实数k的取值范围．
当k=0时，M、N、P三点共线，构不成三角，
∴k≠0，
如图所示，△MNP是直角三角形，有三种情况：
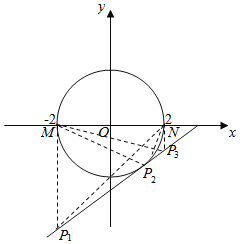
当M是直角顶点时，直线上有唯一点P1点满足条件；
当N是直角顶点时，直线上有唯一点P3满足条件；
当P是直角顶点时，此时至少有一个点P满足条件．
由直径对的圆周角是直角，知直线和以MN为直径的圆有公共点即可，
则
≤2，解得﹣
≤k≤，且k≠0．
∴实数k的取值范围是[﹣，0）∪（0，]．
故选：D．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
