题目内容
【题目】已知![]() 是椭圆
是椭圆![]() :
:![]() (
(![]() )与抛物线
)与抛物线![]() :
:![]() 的一个公共点,且椭圆与抛物线具有一个相同的焦点
的一个公共点,且椭圆与抛物线具有一个相同的焦点![]() .
.
(Ⅰ)求椭圆![]() 及抛物线
及抛物线![]() 的方程;
的方程;
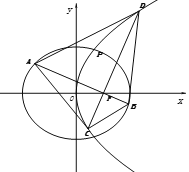
(Ⅱ)设过![]() 且互相垂直的两动直线
且互相垂直的两动直线![]() ,
,![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的最小值.
面积的最小值.
【答案】(Ⅰ)椭圆![]() 的方程为
的方程为![]() ,抛物线
,抛物线![]() 的方程为
的方程为![]() ;(Ⅱ)见解析.
;(Ⅱ)见解析.
【解析】
(Ⅰ)根据![]() 是椭圆
是椭圆![]() :
:![]() (
(![]() )与抛物线
)与抛物线![]() :
:![]() 的一个公共点,可求得
的一个公共点,可求得![]() ,从而可得相同的焦点
,从而可得相同的焦点![]() 的坐标,结合
的坐标,结合![]() ,即可求得
,即可求得![]() 与
与![]() ,从而可得椭圆
,从而可得椭圆![]() 及抛物线
及抛物线![]() 的方程;(Ⅱ)由题可知直线
的方程;(Ⅱ)由题可知直线![]() 斜率存在,设直线
斜率存在,设直线![]() 的方程
的方程![]() ,
,![]() ,当
,当![]() 时,求出
时,求出![]() ,当
,当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,结合韦达定理及弦长公式求得
,结合韦达定理及弦长公式求得![]() 及
及![]() ,表示出
,表示出![]() ,通过换元及二次函数思想即可求得四边形
,通过换元及二次函数思想即可求得四边形![]() 面积的最小值.
面积的最小值.
(Ⅰ)![]() 抛物线
抛物线![]() :
:![]() 一点
一点
![]() ,即抛物线
,即抛物线![]() 的方程为
的方程为![]() ,
,![]()
![]()
又![]() 在椭圆
在椭圆![]() :
:![]() 上
上
![]() ,结合
,结合![]() 知
知![]() (负舍),
(负舍), ![]() ,
,
![]() 椭圆
椭圆![]() 的方程为
的方程为![]() ,抛物线
,抛物线![]() 的方程为
的方程为![]() .
.
(Ⅱ)由题可知直线![]() 斜率存在,设直线
斜率存在,设直线![]() 的方程
的方程![]() ,
,![]()
①当![]() 时,
时,![]() ,直线
,直线![]() 的方程
的方程![]() ,
,![]() ,故
,故![]()
②当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,由
,由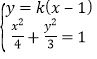 得
得![]() .
.
![]()
由弦长公式知![]()
![]() .
.
同理可得![]() .
.
![]() .
.
令![]() ,则
,则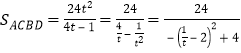 ,当
,当![]() 时,
时,![]() ,
,![]()
综上所述:四边形![]() 面积的最小值为8.
面积的最小值为8.

【题目】为调查中国及美国的高中生在“家”、“朋友聚集的地方”、“个人空间”这三个场所中感到最幸福的场所是哪个,从中国某城市的高中生中随机抽取了55人,从美国某城市高中生中随机抽取了45人进行答题。中国高中生的答题情况:选择“家”的高中生的人数占![]() ,选择“朋友聚集的地方”的高中生的人数占
,选择“朋友聚集的地方”的高中生的人数占![]() ,选择“个人空间”的高中生的人数占
,选择“个人空间”的高中生的人数占![]() ,美国高中生的答题情况:选择“家”的高中生的人数占
,美国高中生的答题情况:选择“家”的高中生的人数占![]() ,选择“朋友聚集的地方”的高中生的人数占
,选择“朋友聚集的地方”的高中生的人数占![]() ,选择“个人空间”的高中生的人数占
,选择“个人空间”的高中生的人数占![]() 。
。
(1)请根据以上调查结果将下面的2X2列联表补充完整,并判断能否有95%的把握认为恋家(在家里感到最幸福)与国别有关;
在家里感到最幸福 | 在其他场所感到最幸福 | 总计 | |
中国高中生 | |||
美国高中生 | |||
总计 |
(2)从被调查的不“恋家”的美国高中生中,用分层抽样的方法随机选出4人接受进一步调查,再从4人中随机选出2人到中国交流学习,求2人中含有在“个人空间”感到最幸福的高中生的概率。
| 0.050 | 0.025 | 0.010 | 0.001 |
| 3.841 | 5.024 | 6.635 | 10.8 |
附: