题目内容
【题目】为回馈顾客,某商场拟通过摸球兑奖的方式对![]() 位顾客进行奖励,规定:每位顾客从一个装有
位顾客进行奖励,规定:每位顾客从一个装有![]() 个标有面值的球的袋中一次性随机摸出
个标有面值的球的袋中一次性随机摸出![]() 个球,球上所标的面值之和为该顾客所获的奖励额.
个球,球上所标的面值之和为该顾客所获的奖励额.
(1)若袋中所装的![]() 个球中有
个球中有![]() 个所标的面值为
个所标的面值为![]() 元,其余
元,其余![]() 个均为
个均为![]() 元,求顾客所获的奖励额的分布列及数学期望;
元,求顾客所获的奖励额的分布列及数学期望;
(2)商场对奖励总额的预算是![]() 元,并规定袋中的
元,并规定袋中的![]() 个球只能由标有面值为
个球只能由标有面值为![]() 元和
元和![]() 元的两种球组成,或标有面值
元的两种球组成,或标有面值![]() 元和
元和![]() 元的两种球组成.为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡.请对袋中的
元的两种球组成.为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡.请对袋中的![]() 个球的面值给出一个合适的设计,并说明理由.
个球的面值给出一个合适的设计,并说明理由.
【答案】(1)(ⅰ)![]() ;(ⅱ)40;(2)选择方案(20,20,40,40).
;(ⅱ)40;(2)选择方案(20,20,40,40).
【解析】
试题(1)(ⅰ)摸出2个球共有![]() 种方法,由题意得摸出2个球中一个为面值为50元,另一个为10元的,所以有
种方法,由题意得摸出2个球中一个为面值为50元,另一个为10元的,所以有![]() 种方法,所求概率为
种方法,所求概率为![]() ;(ⅱ)先确定随机变量取法:20,60.再分别求对应概率,列表得分布列,最后根据公式求数学期望(2)根据商场的预算,每个顾客的平均奖励额为60元,所以数学期望为60元.因此只能有两个方案:(10,10,50,50),(20,20,40,40),这两个方案的数学期望皆为60,为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡,即方差要尽可能小,计算两者方差得选择方案(20,20,40,40).
;(ⅱ)先确定随机变量取法:20,60.再分别求对应概率,列表得分布列,最后根据公式求数学期望(2)根据商场的预算,每个顾客的平均奖励额为60元,所以数学期望为60元.因此只能有两个方案:(10,10,50,50),(20,20,40,40),这两个方案的数学期望皆为60,为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡,即方差要尽可能小,计算两者方差得选择方案(20,20,40,40).
试题解析:(1)设顾客所获的奖励额为X,
(ⅰ)依题意,得P(X=60)=![]() =
=![]() ,
,
即顾客所获的奖励额为60元的概率为![]() .
.
(ⅱ)依题意,得X的所有可能取值为20,60.
P(X=60)=![]() ,P(X=20)==
,P(X=20)==![]() ,
,
即X的分布列为
X | 20 | 60 |
P |
|
|
所以顾客所获的奖励额的期望为
E(X)=20×![]() +60×
+60×![]() =40(元).
=40(元).
(2)根据商场的预算,每个顾客的平均奖励额为60元.所以,先寻找期望为60元的可能方案.对于面值由10元和50元组成的情况,如果选择(10,10,10,50)的方案,因为60元是面值之和的最大值,所以期望不可能为60元;如果选择(50,50,50,10)的方案,因为60元是面值之和的最小值,所以期望也不可能为60元,因此可能的方案是(10,10,50,50),记为方案1.
对于面值由20元和40元组成的情况,同理可排除(20,20,20,40)和(40,40,40,20)的方案,所以可能的方案是(20,20,40,40),记为方案2.
以下是对两个方案的
对于方案1,即方案(10,10,50,50),设顾客所获的奖励额为X1,则X1的分布列为
X1 | 20 | 60 | 100 |
P |
|
|
|
X1的期望为E(X1)=20×![]() +60×
+60×![]() +100×
+100×![]() =60,
=60,
X1的方差为D(X1)=(20-60)2×![]() +(60-60)2×
+(60-60)2×![]() +(100-60)2×
+(100-60)2×![]() =
=![]() .
.
对于方案2,即方案(20,20,40,40),设顾客所获的奖励额为X2,则X2的分布列为
X2 | 40 | 60 | 80 |
P |
|
|
|
X2的期望为E(X2)=40×![]() +60×
+60×![]() +80×
+80×![]() =60,
=60,
X2的方差为D(X2)=(40-60)2×![]() +(60-60)2×
+(60-60)2×![]() +(80-60)2×
+(80-60)2×![]() =
=![]() .
.
由于两种方案的奖励额的期望都符合要求,但方案2奖励额的方差比方案1的小,所以应该选择方案2.

 开心快乐假期作业暑假作业西安出版社系列答案
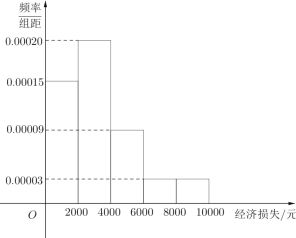
开心快乐假期作业暑假作业西安出版社系列答案【题目】某超强台风登陆海南省.据统计,本次台风造成全省直接经济损失119.52亿元,适逢暑假,小明调查住在自己小区的50户居民由于台风造成的经济损失,作出如下频率分布直方图:
| 经济损失4000元以下 | 经济损失4000元以上 | 合计 |
捐款超过500元 | 30 | ||
捐款低于500元 | 6 | ||
合计 |
台风后区委会号召小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如上表,在表格空白处填写正确数字,并说明是否有![]() 以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关?
以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关?
附:临界值表
| 2.072 | 2.706 | 3.841 | 5.024 | 6635 | 7.879 | 10.828 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
参考公式: ![]() ,
, ![]() .
.
【题目】经销商第一年购买某工厂商品的单价为![]() (单位:元),在下一年购买时,购买单价与其上年度销售额(单位:万元)相联系,销售额越多,得到的优惠力度越大,具体情况如下表:
(单位:元),在下一年购买时,购买单价与其上年度销售额(单位:万元)相联系,销售额越多,得到的优惠力度越大,具体情况如下表:
上一年度 销售额/万元 |
|
|
|
|
|
|
商品单价/元 |
|
|
|
|
|
|
为了研究该商品购买单价的情况,为此调查并整理了![]() 个经销商一年的销售额,得到下面的柱状图.
个经销商一年的销售额,得到下面的柱状图.
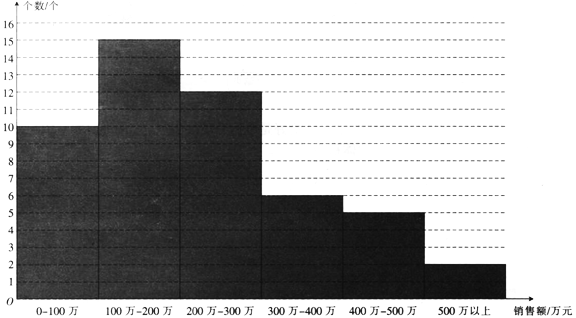
已知某经销商下一年购买该商品的单价为![]() (单位:元),且以经销商在各段销售额的频率作为概率.
(单位:元),且以经销商在各段销售额的频率作为概率.
(1)求![]() 的平均估计值.
的平均估计值.
(2)为了鼓励经销商提高销售额,计划确定一个合理的年度销售额![]() (单位:万元),年销售额超过
(单位:万元),年销售额超过![]() 的可以获得红包奖励,该工厂希望使
的可以获得红包奖励,该工厂希望使![]() 的经销商获得红包,估计
的经销商获得红包,估计![]() 的值,并说明理由.
的值,并说明理由.

