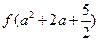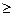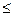题目内容
已知函数f(x)=
:
(1)写出此函数的定义域和值域;
(2)证明函数在(0,+∞)为单调递减函数;
(3)试判断并证明函数y=(x-3)f(x)的奇偶性.
| x+3 |
| x |
(1)写出此函数的定义域和值域;
(2)证明函数在(0,+∞)为单调递减函数;
(3)试判断并证明函数y=(x-3)f(x)的奇偶性.
(1)函数f(x)的定义域为{x|x≠0}.
f(x)=1+
,∴值域为{y|y≠1}.
(2)证明:设0<x1<x2,
则:f(x2)-f(x1)=(1+
)-(1+
)=
-
=
,
∵0<x1<x2,∴x1•x2>0,x1-x2<0,
∴f(x2)-f(x1)<0,即f(x2)<f(x1),
∴函数在(0,+∞)上为单调递减函数.
(3)函数定义域关于原点对称,
设g(x)=(x-3)f(x)=
,
∵g(-x)=
=-g(x),
∴此函数为奇函数.
f(x)=1+
| 3 |
| x |
(2)证明:设0<x1<x2,
则:f(x2)-f(x1)=(1+
| 3 |
| x2 |
| 3 |
| x1 |
| 3 |
| x2 |
| 3 |
| x1 |
| 3(x1-x2) |
| x1•x2 |
∵0<x1<x2,∴x1•x2>0,x1-x2<0,
∴f(x2)-f(x1)<0,即f(x2)<f(x1),
∴函数在(0,+∞)上为单调递减函数.
(3)函数定义域关于原点对称,
设g(x)=(x-3)f(x)=
| x2-9 |
| x |
∵g(-x)=
| x2-9 |
| -x |
∴此函数为奇函数.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目

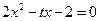 的两根为
的两根为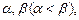 函数
函数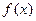 =
=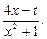
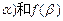 的值. (2).证明:
的值. (2).证明: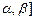 上是增函数.(3).对任意正数
上是增函数.(3).对任意正数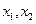 ,求证:
,求证: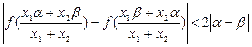
 上的函数
上的函数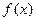 满足下列条件:1对定义域内任意
满足下列条件:1对定义域内任意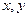 ,恒有
,恒有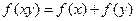 ;2当
;2当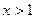 时
时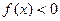 ;3
;3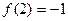 (1)求
(1)求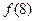 的值;
的值;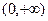 上为减函数;(3)解不等式 :
上为减函数;(3)解不等式 :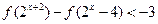
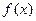 是偶函数,其定义域为
是偶函数,其定义域为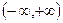 ,且在
,且在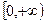 上是减函数,则
上是减函数,则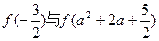 的大小关系是( )
的大小关系是( )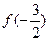 >
>