题目内容
设函数f(x)＝ex＋x－2，g(x)＝ln x＋x2－3.若实数a，b满足f(a)＝0，g(b)＝0，则 ( )．
A．g(a)<0<f(b) B．f(b)<0<g(a)
C．0<g(a)<f(b) D．f(b)<g(a)<0
A
【解析】对于f(x)＝ex＋x－2，f′(x)＝ex＋1>0，f(x)在R上递增，由于f(0)＝e0－2＝－1<0，
f(1)＝e＋1－2＝e－1>0，
∴由f(a)＝0知0<a<1；
对于g(x)＝ln x＋x2－3(x>0)，g′(x)＝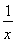
＋2x>0(x>0)，
∴g(x)在(0，＋∞)上递增，
由于g(1)＝－2<0，g(2)＝ln 2＋1>0，
∴由g(b)＝0知1<b<2.
故f(b)>f(1)>0，g(a)<g(1)<0，∴g(a)<0<f(b)．
练习册系列答案
相关题目
