题目内容
过x轴正半轴上一点P的直线与抛物线y2=4x交于两点A、B的横坐标分别为3和 ,若
,若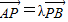 则λ的值等于( )
则λ的值等于( )A.9
B.9或-9
C.3
D.3或-3
【答案】分析:依题意,可求得A、B两点的坐标,从而可求其方程,继而可得点P的坐标,利用向量共线的坐标运算即可求得λ.
解答: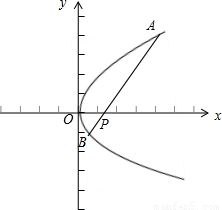 解:依题意,作图如右:
解:依题意,作图如右:
不妨令点A在x轴上方,点B在x轴下方,
∵A、B为抛物线y2=4x上的两点,A、B两点的横坐标分别为3和 ,
,
∴A(3,2 ),B(
),B( ,-
,-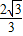 ),
),
∴kAB=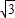 ,
,
∴AB的直线方程为y-2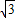 =
=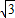 (x-3),令y=0得x=1,
(x-3),令y=0得x=1,
∴P(1,0);
∴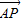 =(1-3,-2
=(1-3,-2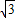 )=(-2,-2
)=(-2,-2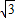 ),
),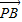 =(-
=(- ,-
,-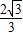 ),
),
∵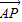 =λ
=λ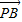 ,
,
∴(-2,-2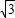 )=λ(-
)=λ(- ,-
,-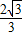 ),
),
∴-2=- λ,解得λ=3;
λ,解得λ=3;
若点A在x轴下方,点B在x轴上方,同理可求kAB=-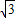 ,P(1,0),
,P(1,0),
此时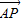 =(
=( ,-
,-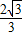 ),
),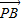 =(2,-2
=(2,-2 ),
),
由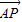 =λ
=λ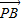 ,得λ=3.
,得λ=3.
综上所述,λ=3.
故选C.
点评:本题考查抛物线的简单性质,考查方程思想与分类讨论思想及运算能力的综合运用,属于中档题.
解答:
 解:依题意,作图如右:
解:依题意,作图如右:不妨令点A在x轴上方,点B在x轴下方,
∵A、B为抛物线y2=4x上的两点,A、B两点的横坐标分别为3和
 ,
,∴A(3,2
 ),B(
),B( ,-
,-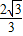 ),
),∴kAB=
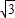 ,
,∴AB的直线方程为y-2
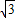 =
=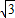 (x-3),令y=0得x=1,
(x-3),令y=0得x=1,∴P(1,0);
∴
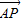 =(1-3,-2
=(1-3,-2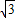 )=(-2,-2
)=(-2,-2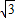 ),
),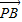 =(-
=(- ,-
,-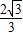 ),
),∵
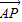 =λ
=λ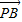 ,
,∴(-2,-2
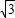 )=λ(-
)=λ(- ,-
,-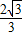 ),
),∴-2=-
 λ,解得λ=3;
λ,解得λ=3;若点A在x轴下方,点B在x轴上方,同理可求kAB=-
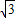 ,P(1,0),
,P(1,0),此时
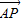 =(
=( ,-
,-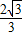 ),
),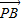 =(2,-2
=(2,-2 ),
),由
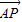 =λ
=λ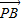 ,得λ=3.
,得λ=3.综上所述,λ=3.
故选C.
点评:本题考查抛物线的简单性质,考查方程思想与分类讨论思想及运算能力的综合运用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知抛物线的顶点在坐标原点O,焦点F在x轴正半轴上,倾斜角为锐角的直线l过F点,设直线l与抛物线交于A、B两点,与抛物线的准线交于M点,
已知抛物线的顶点在坐标原点O,焦点F在x轴正半轴上,倾斜角为锐角的直线l过F点,设直线l与抛物线交于A、B两点,与抛物线的准线交于M点,