题目内容
(2013•大连一模)设离心率e=
的椭圆M:
+
=1(a>b>0)的左、右焦点分别为F1、F2,P是x轴正半轴上一点,以PF1为直径的圆经过椭圆M短轴端点,且该圆和直线x+
y+3=0相切,过点P直线椭圆M相交于相异两点A、C.
(Ⅰ)求椭圆M的方程;
(Ⅱ)若相异两点A、B关于x轴对称,直线BC交x轴与点Q,求Q点坐标.
| 1 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
(Ⅰ)求椭圆M的方程;
(Ⅱ)若相异两点A、B关于x轴对称,直线BC交x轴与点Q,求Q点坐标.
分析:(Ⅰ)设圆所过短轴端点为N,由|NF1|=a,∠PNF1=
,e=
,可判断F2(c,0)是以PF1为直径的圆的圆心,根据圆和直线相切可得2c=
,据此解得c值,从而得到a,b;
(Ⅱ)设点A(x1,y1),C(x2,y2),则点B(x1,-y1),设直线PA的方程为y=k(x-3),代入椭圆方程消掉y得x的二次方程,写出直线BC的方程,令y=0可得点Q的横坐标,代入韦达定理即可求得其值,从而得到点Q的坐标;
| π |
| 2 |
| 1 |
| 2 |
| |c+3| | ||||
|
(Ⅱ)设点A(x1,y1),C(x2,y2),则点B(x1,-y1),设直线PA的方程为y=k(x-3),代入椭圆方程消掉y得x的二次方程,写出直线BC的方程,令y=0可得点Q的横坐标,代入韦达定理即可求得其值,从而得到点Q的坐标;
解答:解:(Ⅰ)设以PF1为直径的圆经过椭圆M短轴端点N,
∴|NF1|=a,∠PNF1=
,∵e=
,∴a=2c,
∴∠NF1P=
,|F1P|=2a.
∴F2(c,0)是以PF1为直径的圆的圆心,
∵该圆和直线x+
y+3=0相切,
∴2c=
,
∴c=1,a=2,b=
,
∴椭圆M的方程为:
+
=1.
(Ⅱ)设点A(x1,y1),C(x2,y2),则点B(x1,-y1),
设直线PA的方程为y=k(x-3),联立方程组
,
化简整理得(4k2+3)x2-24k2x+36k2-12=0,
由△=(24k2)2-4•(3+4k2)•(36k2-12)>0得k2<
.
则x1+x2=
,x1x2=
.
直线BC的方程为:y+y1=
(x-x1),
令y=0,则x=
=
=
=
,
∴Q点坐标为(
,0).
∴|NF1|=a,∠PNF1=
| π |
| 2 |
| 1 |
| 2 |
∴∠NF1P=
| π |
| 3 |
∴F2(c,0)是以PF1为直径的圆的圆心,
∵该圆和直线x+
| 3 |
∴2c=
| |c+3| | ||||
|
∴c=1,a=2,b=
| 3 |
∴椭圆M的方程为:
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)设点A(x1,y1),C(x2,y2),则点B(x1,-y1),
设直线PA的方程为y=k(x-3),联立方程组
|
化简整理得(4k2+3)x2-24k2x+36k2-12=0,
由△=(24k2)2-4•(3+4k2)•(36k2-12)>0得k2<
| 3 |
| 5 |
则x1+x2=
| 24k2 |
| 4k2+3 |
| 36k2-12 |
| 4k2+3 |
直线BC的方程为:y+y1=
| y2+y1 |
| x2-x1 |
令y=0,则x=
| y1x2+y2x1 |
| y1+y2 |
| 2x1x2-3(x1+x2) |
| x1+x2-6 |
| ||||
|
| 4 |
| 3 |
∴Q点坐标为(
| 4 |
| 3 |
点评:本题考查直线方程、椭圆方程及其位置关系,考查学生对问题的分析解决能力,韦达定理、判别式是常用内容,要牢固掌握.

练习册系列答案
相关题目
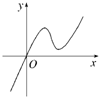 (2013•大连一模)定义在R上的函数f(x)满足f(3)=1,f(-2)=3,f′(x)为f(x)的导函数,已知y=f′(x)的图象如图所示,且f′(x)有且只有一个零点,若非负实数a,b满足f(2a+b)≤1,f(-a-2b)≤3,则
(2013•大连一模)定义在R上的函数f(x)满足f(3)=1,f(-2)=3,f′(x)为f(x)的导函数,已知y=f′(x)的图象如图所示,且f′(x)有且只有一个零点,若非负实数a,b满足f(2a+b)≤1,f(-a-2b)≤3,则