题目内容
【题目】图1是直角梯形![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() ,
,![]() ,以
,以![]() 为折痕将
为折痕将![]() 折起,使点
折起,使点![]() 到达
到达![]() 的位置,且
的位置,且![]() ,如图2.
,如图2.


(1)证明:平面![]() 平面
平面![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)在图1中,连结![]() ,根据
,根据![]() 且
且![]() ,得到四边形
,得到四边形![]() 为菱形,则
为菱形,则![]() ,在图2中,由
,在图2中,由 ![]() ,得到
,得到![]() ,利用线面垂直的判定定理得到
,利用线面垂直的判定定理得到![]() 面
面![]() ,再利用面面垂直的判定定理证明平面
,再利用面面垂直的判定定理证明平面![]() 平面
平面![]() .
.
(2)取![]() 中点
中点![]() ,连接
,连接![]() ,设点
,设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,易证
,易证![]() 平面
平面![]() ,则
,则![]() ,且
,且![]() ,再由(1)
,再由(1)![]() 面
面![]() ,利用等体积法
,利用等体积法![]() 求解.
求解.
(1)如图所示:


证明:在图1中,连结![]() ,由已知得
,由已知得![]() ,
,
∵![]() 且
且![]() ,
,
∴四边形![]() 为菱形,
为菱形,
连结![]() 交
交![]() 于点
于点![]() ,
,
∴![]() ,
,
又∵在![]() 中,
中,![]() ,
,
∴![]() ,
,
在图2中,![]() ,
,
∵![]() ,∴
,∴![]() ,
,
由题意知![]() ,
,
∴![]() 面
面![]() ,又
,又![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ;
;
(2)如图,

取![]() 中点
中点![]() ,连接
,连接![]() ,设点
,设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
在直角梯形![]() 中,
中,![]() 为中位线,则
为中位线,则![]() ,
,
由(1)得![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() ,又
,又![]()
得![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
所以![]() ,且
,且![]() ,
,
在三棱锥![]() 中,
中,![]() ,
,
即![]() ,
,
所以 ,
,
即点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.

【题目】为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援,现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.

(1)求出易倒伏玉米茎高的中位数![]() ;
;
(2)根据茎叶图的数据,完成下面的列联表:
抗倒伏 | 易倒伏 | |
矮茎 | ||
高茎 |
(3)根据(2)中的列联表,是否可以在犯错误的概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?
附: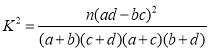 ,
,
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【题目】2019年底,湖北省武汉市等多个地区陆续出现感染新型冠状病毒肺炎的患者.为及时有效地对疫情数据进行流行病学统计分析,某地研究机构针对该地实际情况,根据该地患者是否有武汉旅行史与是否有确诊病例接触史,将新冠肺炎患者分为四类:有武汉旅行史(无接触史),无武汉旅行史(无接触史),有武汉旅行史(有接触史)和无武汉旅行史(有接触史),统计得到以下相关数据.
(1)请将列联表填写完整:
有接触史 | 无接触史 | 总计 | |
有武汉旅行史 | 27 | ||
无武汉旅行史 | 18 | ||
总计 | 27 | 54 |
(2)能否在犯错误的概率不超过0.025的前提下认为有武汉旅行史与有确诊病例接触史有关系?
附:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【题目】某周末,郑州方特梦幻王国汇聚了八方来客.面对该园区内相邻的两个主题公园“千古蝶恋”和“西游传说”,成年人和未成年人选择游玩的意向会有所不同.某统计机构对园区内的100位游客(这些游客只在两个主题公园中二选一)进行了问卷调查.调查结果显示,在被调查的50位成年人中,只有10人选择“西游传说”,而选择“西游传说”的未成年人有20人.
(1)根据题意,请将下面的![]() 列联表填写完整;
列联表填写完整;
选择“西游传说” | 选择“千古蝶恋” | 总计 | |
成年人 | |||
未成年人 | |||
总计 |
(2)根据列联表的数据,判断是否有![]() 的把握认为选择哪个主题公园与年龄有关.
的把握认为选择哪个主题公园与年龄有关.
附参考公式与表: (
(![]() ).
).
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |



